На рисунке отрезки AB и CD пересекаются в точке О. Отрезок ОB равен отрезку ОC,а угол B равен углу C. Докажите что отрезок ОА равен углу DО.
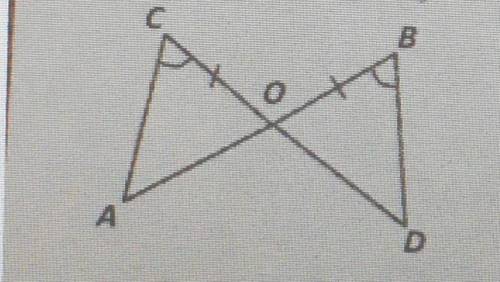
Другие вопросы по теме Геометрия
Популярные вопросы
- Характеристика царицы(мачехи) из сказки о семи богатырях. зарание...
3 - Скажите,берут ли с базой, и обществом на какую-нибудь специальность...
3 - Скорзини взяли 3 яблока, потом 1/3 от остатка, потом еще 3, после...
3 - Мое мнение о поступках дон пол тетрадной стр)...
2 - Асан выписал все трехзначные числа. а из выписанных чисел есен стер...
2 - Знайдіть швидкість автомобіля, якщо за 7\9 години він подолав п’ятдесят...
1 - Эссе на тему о чем говорят морфемы...
2 - Построить график этой функции y= |x|+|x-3|,их будет два,так как модуль...
1 - Вставьте н или нн. 1. ракета запуще..а в космос. - квартира запуще..а...
3 - 1.спиши словосочетания, в скобках укажи падеж. 1. появился (на чём?...
1
По условию, отрезок ОB равен отрезку ОC.
По свойству равенства отрезков, если два отрезка равны, то они могут заменять друг друга в любом равенстве, т.е. можно использовать отрезок ОB вместо отрезка ОC и наоборот.
Также, по условию, угол B равен углу C.
По свойству равенства углов, если два угла равны, то они могут заменять друг друга в любом равенстве, т.е. можно использовать угол B вместо угла C и наоборот.
Исходя из этой информации, мы можем заменить отрезок ОC отрезком ОB и угол C углом B, получив равенство:
Отрезок ОА равен углу DО,
а отрезок ОB равен отрезку ОC и угол B равен углу C.
Теперь для доказательства равенства отрезка ОА и угла DО мы можем использовать теорему о равенстве углов, которая гласит: "если два угла истреугольника равны двум углам другого треугольника соответственно, то третий угол первого треугольника равен третьему углу второго треугольника".
Применим эту теорему для нашей ситуации. Предварительно заменим угол C углом B и отрезок ОC отрезком ОB:
Треугольник ОАО прямоугольный, так как две его стороны (отрезки ОА и ОО) являются радиусами окружности, а третья сторона (отрезок АО) является диаметром, а значит против прямого угла DО будет также прямой угол О.
Таким образом, мы доказали, что отрезок ОА равен углу DО.