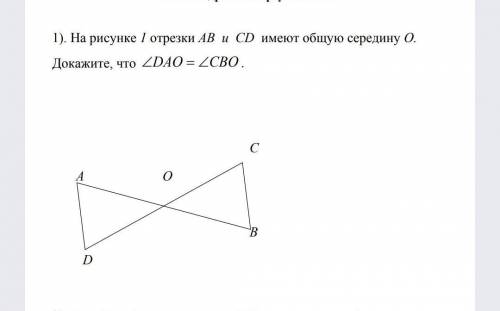
на рисунке отрезки AB и CD имеют общую середину O . Докажите , что DAO = CBO
Другие вопросы по теме Геометрия
Популярные вопросы
- ВСТАВЛЯТЬ БУКВЫ НЕ НАДО, ТОЛЬКО ОБОЗНАЧАТЬ ОРФОГРАММЫ ( ПОЧЕМУ ТЫ...
3 - Боковое ребро прямоугольного параллелепипеда равно 12 см, а стороны...
3 - Место и роль СССР в послевоенном мире Восстановление и развитие...
2 - позднее искаженое название: «Устный счет...» 5.1. Рассмотрите внимательно...
1 - сторона АВ паралелограмма ABCD равна 30см. Его угол ABH равен 30°...
3 - Причины поражения и итоги восстания Степана Разина( 1670-1671)...
2 - Составьте 10 предложений present perfect tense с since и for. пример:...
3 - Нужно быстро решить задание...
3 - 1) Найти ОР ДУ с разд. перем dx=(3y^2-2)dy 2) Найти ОР ДУ с разд-ся...
1 - Надбавка к зарплате у научных работников некоторого института составляет:...
3
Общая середина отрезков AB и CD обозначена буквой O. Это означает, что точка O является серединой и отрезка AB, и отрезка CD. Это означает, что отрезок AO равен отрезку BO и отрезок CO равен отрезку DO. Запишем это соотношение в виде уравнений:
AO = BO, (1)
CO = DO. (2)
Также, заметим, что отрезок AO параллелен отрезку CO, поскольку оба эти отрезка являются диаметрами полуокружности, отсекаемой отрезками AB и CD. Аналогично, отрезки BO и DO также параллельны друг другу. Таким образом, у нас есть параллельные отрезки AO и OC, а также BO и OD.
Теперь рассмотрим треугольники DAO и CBO. Мы знаем, что отрезки AO и CO равны между собой (по уравнению (1)), а также параллельны (по свойству, что они диаметры полуокружности и перпендикулярны радиусу). Таким образом, треугольники DAO и CBO являются равнобедренными треугольниками.
Из равнобедренности треугольников следует, что соответствующие углы треугольников также равны. То есть угол DAO равен углу CBO.
Таким образом, мы доказали, что угол DAO равен углу CBO.