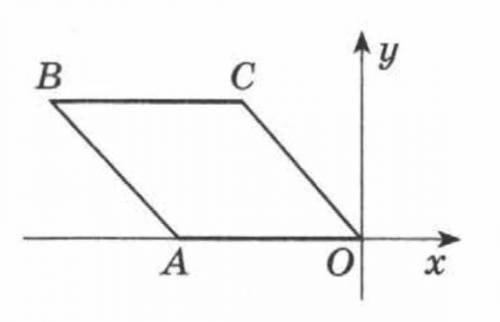
На рисунке OABC — ромб, сторона которого равна 10, высота равна 8. Найдите абсциссу точки В.
Другие вопросы по теме Геометрия
Популярные вопросы
- Вычислить относительную плотность гелия по водороду и по воздуху (н.у)...
2 - Астана-озық идеялар ордасы...
3 - 11!1!1!1 Сплав из никеля меди содержит 45 кг никеля и 30 кг меди. В каком...
2 - Как вы понимаете выражение - короткая, но дивная пора ?...
3 - Задания: 1. Прочитай текст, определи основную мысль текста Можно учиться...
1 - Опишите эту картину . Желательно на английском, но можно и не русском....
2 - Спортивний молот масою 8 кілограмОбертається в горизонтальній площині...
1 - ОГРОМНОЕ ЗАРАНЕЕ РЕБЯТА ПИШИТЕ ИМЕННО ЧТО , ПРО ДРУГИЕ РЕМЕСЛА НЕ ОБЯЗАТЕЛЬНО...
3 - зробити лист як я боліла два тижня тому...
2 - №3 тапсырма. Белгілі бір мекендегі шипалы өсімдіктер туралы (30-35 сөз...
3
Как найти абсциссу и ординату точки на координатной плоскости? Чтобы найти абсциссу, нужно по оси x выбрать то число, которое указано в координатах на первом месте. Чтобы найти ординату, нужно по оси y выбрать то число, которое указано в координатах на втором мест
Свойство №1: В ромбе противоположные стороны равны.
В данном случае, сторона ОА равна 10, поэтому и сторона ОС тоже равна 10.
Свойство №2: В ромбе диагонали перпендикулярны между собой.
Это значит, что ОА и ВС являются перпендикулярными.
Свойство №3: В ромбе диагонали пересекаются в точке, делящей каждую диагональ пополам.
Обозначим точку пересечения диагоналей ромба как М.
Так как ОМ является высотой ромба, а ромба имеет равнобедренную форму, то М является серединной точкой основания ОС.
Мы знаем, что ОС равна 10, поэтому ОМ равна половине стороны ОС, то есть 10/2 = 5.
Теперь мы можем использовать теорему Пифагора для вычисления абсциссы точки В.
Так как ОМ является высотой ромба, а ОВ является биссектрисой угла О, то мы можем рассматривать треугольник ОМВ как прямоугольный треугольник.
Применяя теорему Пифагора к треугольнику ОМВ, мы можем записать следующее:
(АВ)^2 = (ОМ)^2 + (ОВ)^2
(АВ)^2 = 5^2 + 8^2
(АВ)^2 = 25 + 64
(АВ)^2 = 89
Теперь найдем квадратный корень от обеих сторон этого уравнения, чтобы получить абсциссу точки В:
(АВ) = √89
Таким образом, абсцисса точки В равна √89.