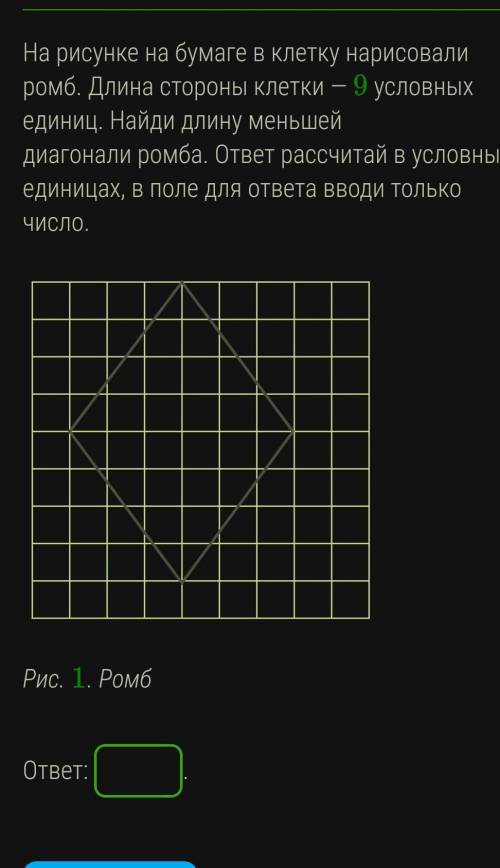
На рисунке на бумаге в клетку нарисовали ромб. Длина стороны клетки — 9 условных единиц. Найди длину меньшей диагонали ромба. ответ рассчитай в условных единицах, в поле для ответа вводи только число.
Другие вопросы по теме Геометрия
Популярные вопросы
- Прочитайте текст историка М.Н.Барышникова и заполните пропуски, используя интернет-ресурсы....
3 - 6 4/3 надо превратить в десятичную...
2 - Р.4. Вычисли.а) 39 + 2390 + 20...
1 - II. Опираясь на текст учебника (с. 17-18), определи и кратко охарактеризуй основные...
2 - Расскажите (придумайте) занимательную историю, которая произошла или могла бы произойти...
2 - Прочитать текст и письменно ответить на вопросы (по тексту) 1. В чём находят своё...
3 - Определите, какое количество информации содержит слово Информатика , если считать,...
2 - информатика 7класс ответ дела перевода из одних единиц измирения информацый в другие...
2 - Два мотоциклиста одновременно выехали из одного города в противоположных направлениях....
3 - Что такое? А. персидская державаБ. Древняя Египет В. ФиникияГ. Древняя Индия ...
1
Чтобы найти длину меньшей диагонали ромба, нам понадобится использовать свойства ромба. Один из таких принципов гласит, что диагонали ромба перпендикулярны друг другу и делят его на четыре равных треугольника.
В данном случае, если длина стороны клетки равна 9 условным единицам, то и длина стороны ромба также будет 9 условных единиц.
Чтобы найти длину меньшей диагонали, нам нужно знать значения длин сторон треугольника, образованного одной из диагоналей и двумя сторонами ромба.
Для нахождения этой длины, мы можем воспользоваться теоремой Пифагора, которая гласит: длина квадрата гипотенузы равна сумме квадратов длин катетов.
В нашем случае, две стороны ромба могут быть рассмотрены как катеты, а диагональ — как гипотенуза треугольника.
Итак, длина одной стороны ромба равна 9 условным единицам. Мы должны найти длину меньшей диагонали, которую обозначим как "d".
Применим теорему Пифагора для нахождения "d":
d² = 9² + 9²
d² = 81 + 81
d² = 162
Теперь извлечем корень из обеих сторон уравнения, чтобы найти длину меньшей диагонали:
d = √162
Поскольку в задаче требуется ответ в условных единицах, мы можем оставить его в этом виде.
Меньшую диагональ ромба можно представить как "d ≈ √162 условных единиц".
Это ответ, который нужно ввести в поле для ответа.