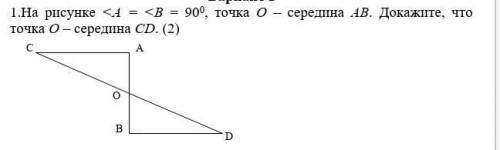
На рисунке <А = <В = 90°, точка О – середина АВ. Докажите, что точка О – середина CD. (2) сделайте

Для начала, нам нужно разобраться с данными на рисунке и сформулировать условие, которое нам надо доказать.

На рисунке даны два прямоугольных треугольника ABC и CDE. Углы А и В обозначены специальным символом "<" и равны 90 градусам. Точка О – середина отрезка AB.

Нам нужно доказать, что точка О также является серединой отрезка CD.

Для решения этой задачи воспользуемся свойствами параллелограммов.

Обратим внимание, что мы можем провести две пары параллельных прямых линий: AB || CD и BC || DE (это общее свойство прямоугольников).

Также обратим внимание, что точка О является серединой отрезка AB, значит, AO = OB.

Теперь проведем медианы в треугольниках ABC и CDE, обозначив середины сторон треугольников как F и G соответственно.

Так как О - середина AB, то OF = FB. А также, по свойству медианы, OF || AB. А именно, треугольник OCX (треугольник ROC) является подобным треугольнику ОFА (треугольнику OFB).

Аналогично, так как точка G - середина CD, то DG = GE и DG || CD. Здесь треугольник RC’X (треугольник ROC) подобен треугольнику GC’E (треугольнику GDC).

Теперь рассмотрим соотношения между этими треугольниками:

1) Разделим длины соответствующих сторон:

OC / ОF = CX / FA (из подобия OCX и ОFА)
RC / GC’ = CX / GE (из подобия RC’X и GC’E)

2) Так как точка О - середина AB, то FA = FB, а следовательно, CX = a/2 (так как полная длина CD = a)

3) Также, так как точка G - середина CD, то GE = DG, а следовательно, CX = b/2 (так как полная длина CD = b)

4) Так как ОC = CR (параллельность прямых AB и CD), то OC / RC = 1.

Теперь применим эти равенства:

OC / ОF = CX / FA = (a/2) / (a/2) = 1 (1)

RC / GC’ = CX / GE = (b/2) / (b/2) = 1 (2)

Из равенств (1) и (2) мы видим, что OC / ОF = RC / GC’.

Но так как ОС=CR (пункт 4), то и OC / ОF = RC / GC'.

А это значит, что треугольники ROC и GDC подобны.

Из подобия треугольников следует, что OD / GD = OC / RC (соотношение длин сторон параллельных сторон подобных треугольников).

Но OC / RC = 1 (пункт 4).

Поэтому OD / GD = 1.

Значит, OD = GD.

Таким образом, мы доказали, что точка О - середина CD.

Подведем итоги:

Дана прямоугольная треугольник AB, в котором AO = OB.
Требуется доказать, что точка О является серединой отрезка CD.
Для решения задачи мы воспользовались свойствами параллелограммов и подобными треугольниками.
Мы провели медианы в треугольниках и воспользовались соотношениями длин сторон подобных треугольников.
В результате получили, что OD = GD, что доказывает, что точка О - середина CD.