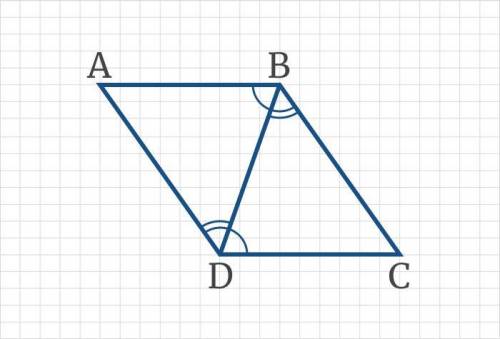
На рисунке изображены ∆CDB и ∆АВD, ∠ABD = ∠CDB,∠ADB = ∠DBC, DC = 5см, ∠A = 50°, BC = 7см. Установите соответствие между равными элементами треугольников.

Добрый день! Давайте разберемся с этой задачей.

Мы имеем два треугольника: ∆CDB и ∆АВD. В нашем условии говорится, что угол ABD равен углу CDB, а угол ADB равен углу DBC. Также нам даны несколько сторон: DC = 5 см и BC = 7 см.

Нам нужно найти соответствие между равными элементами треугольников. Прежде чем мы это сделаем, давайте определим, какие элементы треугольников мы можем считать равными.

У нас есть две пары углов, и они равны друг другу. Мы также можем доказать равенство противоположных сторон треугольников, используя теорему о равенстве углов, так как у нас есть две пары равных углов.

Теперь, обратимся к изображению. Мы видим, что сторона DC обозначена как 5 см, и сторона BC обозначена как 7 см. Мы можем сказать, что сторона AD и сторона CD равны, так как они противоположны равным углам ABD и CDB. Таким образом, AD также равно 5 см.

Также, у нас есть сторона AB, которая не отображается на рисунке. Чтобы найти ее длину, нам нужно использовать теорему косинусов для треугольника ∆ABD, так как у нас есть известные значения двух сторон и угла между ними.

Теорема косинусов гласит: c^2 = a^2 + b^2 - 2ab*cos(C), где c - сторона противолежащая углу C, а a и b - стороны, образующие угол C.

Мы знаем, что сторона AD равна 5 см, сторона CD равна 5 см, и угол ADB равен углу DBC. Поэтому мы можем записать:

AB^2 = AD^2 + BC^2 - 2*AD*BC*cos(ADB)

Подставим значения:

AB^2 = 5^2 + 7^2 - 2*5*7*cos(ADB)

AB^2 = 25 + 49 - 70*cos(ADB)

AB^2 = 74 - 70*cos(ADB)

Теперь мы должны найти значение cos(ADB). Мы знаем угол ADB и можем использовать таблицу значений косинуса. В условии задачи не дано значение этого угла, поэтому в таблице нам нужно найти значение для угла 50°, так как в задаче у нас есть угол A равный 50°. Значение косинуса для этого угла составляет 0,6428.

Теперь, подставим значение косинуса в уравнение:

AB^2 = 74 - 70*0,6428

AB^2 = 74 - 44,996

AB^2 = 29,024

AB ≈ √29,024

AB ≈ 5,39 см

Таким образом, мы можем сказать, что сторона AB равна примерно 5,39 см.

Итак, чтобы ответить на вопрос и установить соответствие между равными элементами треугольников, мы получаем:

∠ABD = ∠CDB
∠ADB = ∠DBC
AD = CD = 5 см
AB ≈ 5,39 см

Надеюсь, что я подробно и понятно объяснил решение этой задачи! Если у вас есть еще вопросы, пожалуйста, задавайте!