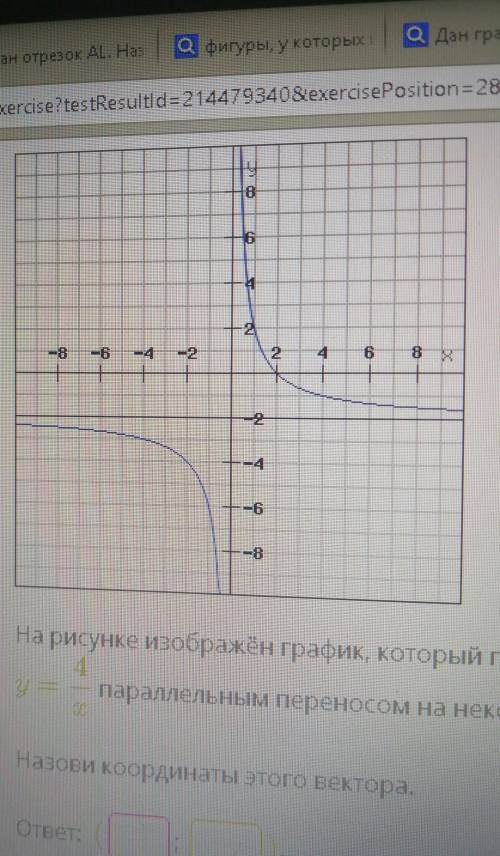
На рисунке изображён график, который получен из графика обратной пропорциональности y=4/x параллельным переносом на некоторый вектор.  

Назови координаты этого вектора.

 

ответ:  (; ).​

Чтобы решить эту задачу, мы должны понять, что произошло с графиком функции y=4/x.

Первоначально, функция y=4/x представляет собой гиперболу, проходящую через начало координат (0,0). Значения функции увеличиваются с ростом x и уменьшаются с увеличением x, что демонстрируется характерными кривыми.

В данной задаче график был получен из исходной функции y=4/x путем параллельного переноса на некоторый вектор. То есть, для каждой точки на графике исходной функции было добавлено одно и то же число к обоим координатам этой точки.

Давайте рассмотрим пример. Возьмем точку (2, 1) на исходном графике. Если мы добавим, например, вектор (3, 4) к этой точке, то получим точку с новыми координатами (2+3, 1+4), то есть (5, 5). Поэтому точка (5, 5) будет соответствовать точке (2, 1) после параллельного переноса на вектор (3, 4).

Чтобы найти координаты вектора параллельного переноса, необходимо взять произвольную точку на исходном графике и вычесть из ее координат соответствующие координаты точки на новом графике (то есть координаты, которые получились после параллельного переноса).

На рисунке изображены две такие точки: (2, 1) и (4, 0.5). Мы можем взять любую из них. Давайте возьмем точку (2, 1).

Теперь нам нужно найти координаты этой точки на новом графике. Интересно отметить, что эта точка на новом графике находится на расстоянии (параллельно оси x) от исходного графика вправо или влево.

Так как точка (2, 1) находится слева от исходного графика, то точка на новом графике будет находиться слева от данной точки (2, 1). Поэтому мы должны вычесть из координаты x нашей точки на исходном графике.

Следовательно, координаты параллельного переноса должны быть вида (-2, ?), где ? - представляет некоторое число, которое мы должны определить.

Теперь, когда у нас есть координаты параллельного переноса вида (-2, ?), давайте рассмотрим вторую точку (4, 0.5) на рисунке и выполним аналогичные действия.

Мы замечаем, что данная точка (4, 0.5) находится справа от исходного графика. Поэтому, чтобы найти координаты параллельного переноса, мы должны вычесть из координаты x этой точки на исходном графике. То есть, координаты будут иметь вид (? -4, ?).

Таким образом, мы получили две пары координат для вектора параллельного переноса: (-2, ?) и (? -4, ?). Вместо ? должны быть числа, которые зависят от расположения точек на новом графике.

Теперь нужно вернуться к исходному уравнению для функции обратной пропорциональности y=4/x и проверить его с помощью найденного вектора параллельного переноса.

Уравнение y=4/x говорит нам, что когда значение x растет (или уменьшается), значение y уменьшается (или растет) обратно пропорционально.

Если мы перенесем исходный график на найденный вектор параллельного переноса, то форма графика должна оставаться неизменной, а только местоположение точек на графике изменится.

Таким образом, используя полученный вектор и диаграмму нового графика, можно найти точки, которые будут соответствовать точкам исходной функции.

К сожалению, без изображения диаграммы нового графика я не могу определить точные значения координат вектора параллельного переноса. Но, я могу сказать, что одна пара координат будет (-2, ?), а вторая будет (? -4, ?), где ? - какое-то число.

Таким образом, ответ на вопрос "Назови координаты этого вектора" будет "(-2, ?) и (? -4, ?)" в зависимости от нового графика, полученного из графика обратной пропорциональности y=4/x путем параллельного переноса на некоторый вектор.