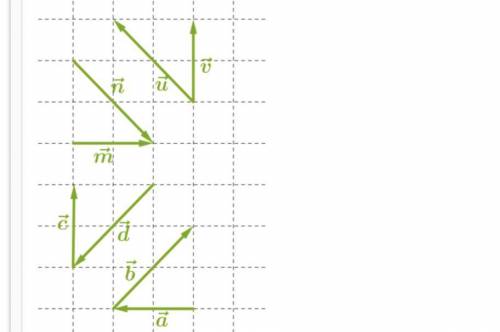
На рисунке даны векторы. Известно, что сторона клетки равна 2 ед. изм. Определи скалярное произведение векторов:

1. C→⋅d→=?

2. A→⋅m→=?

3. U→⋅b→=?

Добрый день! Рад помочь вам разобраться с этим вопросом. Давайте посмотрим на каждое задание по отдельности и найдем скалярные произведения.

1. C→⋅d→:
Для начала посмотрим на вектор C→. Вектор C→ направлен по горизонтали и его длина равна 3 клеткам. Зная, что каждая клетка имеет длину 2 единицы, мы можем определить, что длина вектора C→ равна 2 * 3 = 6 единицам.

Теперь посмотрим на вектор d→. Вектор d→ направлен по вертикали и его длина также равна 3 клеткам. Следовательно, длина вектора d→ равна 2 * 3 = 6 единицам.

Скалярное произведение двух векторов находится по формуле: A→⋅B→ = |A| * |B| * cos(α), где |A| и |B| - длины векторов A→ и B→ соответственно, α - угол между векторами A→ и B→.

Так как векторы C→ и d→ направлены по перпендикулярным осям, угол между ними равен 90 градусам или π/2 радиан. Подставим значения в формулу:

C→⋅d→ = |C| * |d| * cos(π/2) = 6 * 6 * cos(π/2) = 36 * 0 = 0

Таким образом, скалярное произведение векторов C→ и d→ равно 0.

2. A→⋅m→:
Повторим тот же алгоритм для векторов A→ и m→. Вектор A→ направлен вертикально и его длина составляет 4 клетки, что равно 2 * 4 = 8 единицам. Вектор m→ направлен по диагонали и его длина равна 5 клеткам, что составляет 2 * 5 = 10 единиц.

Опять же, так как векторы A→ и m→ образуют угол 90 градусов или π/2 радиан, подставим значения в формулу:

A→⋅m→ = |A| * |m| * cos(π/2) = 8 * 10 * cos(π/2) = 80 * 0 = 0

Скалярное произведение векторов A→ и m→ также равно 0.

3. U→⋅b→:
Также поступим со векторами U→ и b→. Вектор U→ направлен по диагонали и его длина составляет 5 клеток, что равно 2 * 5 = 10 единицам. Вектор b→ направлен горизонтально и его длина равна 4 клеткам, что равно 2 * 4 = 8 единицам.

Угол между векторами U→ и b→ также составляет 90 градусов или π/2 радиан. Подставим значения в формулу:

U→⋅b→ = |U| * |b| * cos(π/2) = 10 * 8 * cos(π/2) = 80 * 0 = 0

Таким образом, скалярное произведение векторов U→ и b→ также равно 0.

Итак, мы получили, что скалярное произведение векторов C→⋅d→, A→⋅m→ и U→⋅b→ равно 0 во всех трех случаях.