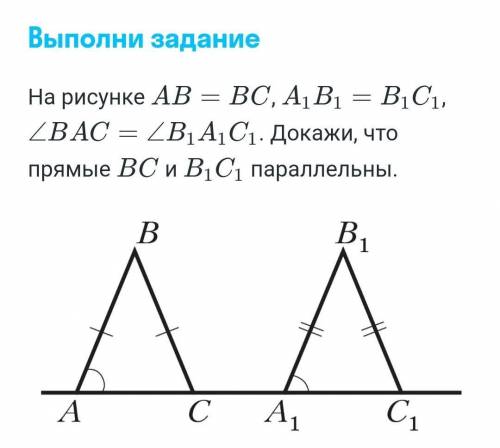
На рисунке АВ = ВС, А В1 = В1С1, C1, /BAC = ZB1.A1 C1. Докажи, что прямые ВС и В1С1 параллельны. B1
Другие вопросы по теме Геометрия
Популярные вопросы
- Чоставте предложение он траву и усердно махал ел только хвостом...
3 - Какого склонения слово учитель? почему...
1 - Найдите a\b, если (3а+9b)\(3b+9а)=-8...
2 - Для посева заготовили семена ячменя, овса,проса-всего 220т 5ц. ячменя...
2 - Основание равнобедренной трапеции равна 12и 24, а ее периметр равен...
1 - Водной кучке лежит 171 камешек , а в другой - 172 камешка.игроку за...
1 - Как называют этих людей которые работают на метеостанциях....
2 - Вынести за скобки общий множитель: 10у в кубе +2у...
3 - Какой объем (в литрах) хлороводорода нужно взять для приготовление...
1 - Язык сделайте 5 предложений на тему что я буду делать на выходных не...
1
Шаг 1: Из рисунка видно, что отрезки АВ и ВС равны (АВ = ВС) и отрезки АВ1 и В1С1 также равны (АВ1 = В1С1). Это означает, что у нас есть два треугольника, АВС и АВ1С1, в которых две стороны равны.
Шаг 2: Теперь мы знаем, что БА=ВС и В1А=В1С1. Это говорит о том, что у нас есть две пары вершин треугольников АВС и АВ1С1, которые соответственно равны. Это основа для того, чтобы сказать, что у треугольников АВС и АВ1С1 также равны соответствующие углы.
Шаг 3: Мы имеем равные углы БАС и В1А1С1. Они находятся между одноименными сторонами ВС и В1С1. Если углы между одноименными сторонами двух параллельных прямых равны, то сами прямые также параллельны.
В результате, мы доказали, что прямые ВС и В1С1 параллельны на основании равенства сторон и углов в треугольниках АВС и АВ1С1.
Надеюсь, что это понятно! Если у вас есть дополнительные вопросы, не стесняйтесь задавать!