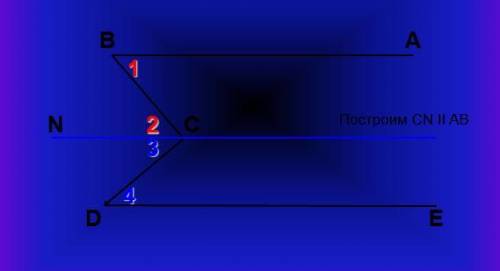
На рисунке АВ II ЕD.
Докажите, что ∠ ВСD = ∠B + ∠D
Другие вопросы по теме Геометрия
Популярные вопросы
- Верны ли следующие суждения об отклоняющемся поведении? a.прояаления...
1 - Пришла зима выпал первый снег пушистое одеяло укрыло землю спит под...
2 - Расстояние между посёлок и городом 150 в 8 часов автобус вышел из...
3 - Укажите ключевые слова в 3 предложении . как они ответить на вопрос...
3 - Ex.4. ответьте на вопросы, употребляя страдательный залог. 1.where...
3 - 100 паскаль авс не проблема могу добасить найти среднее арифметическое...
1 - Какую роль в жизни индийцев играла община...
1 - Чередующаяся гласная есть в слове: лесник‚полевой‚переводить‚прилагательное...
1 - Дроби к общиму общиму знаменателю и сравине их 3/4 5/6...
2 - Заказ на изготовление деталей рабочий выполнил за 3 дня. в первый...
2
На рисунке даны две пары параллельных прямых: AB и ED, а также BC и CD.
∠ВСD обозначает угол между линиями BC и CD. А ∠B обозначает угол между линиями AB и BC, а ∠D - угол между линиями AD и CD.
Теперь, нам нужно доказать, что ∠ ВСD равен сумме углов ∠B и ∠D.
Давай начнем с того, что заметим, что углы ∠BCD и ∠CDA образуют смежные углы.
Закон смежных углов (или Закон вертикальных углов) гласит, что если две прямые пересекаются, то смежные углы равны.
Таким образом, у нас есть уравнение: ∠BCD = ∠CDA.
Используя свойство транзитивности равенства, мы можем записать, что ∠CDA = ∠CD + ∠D.
Теперь, мы знаем, что угол ∠BCD равен ∠CDA, так что мы можем заменить ∠CDA на ∠BCD в уравнении.
Таким образом, у нас получается: ∠ВСD = ∠CD + ∠D.
Используя коммутативное свойство сложения, мы можем переставить слагаемые ∠CD и ∠D:
∠ВСD = ∠D + ∠CD.
Теперь, мы видим, что у нас есть уравнение ∠ВСD = ∠D + ∠CD, которое точно такое же, как ∠ВСD = ∠B + ∠D.
Мы знаем, что ∠B равен ∠CD.
Таким образом, мы можем заменить ∠CD на ∠B в уравнении ∠ВСD = ∠D + ∠CD.
Итак, мы получаем: ∠ВСD = ∠B + ∠D.
Таким образом, мы доказали, что ∠ВСD равен сумме углов ∠B и ∠D.