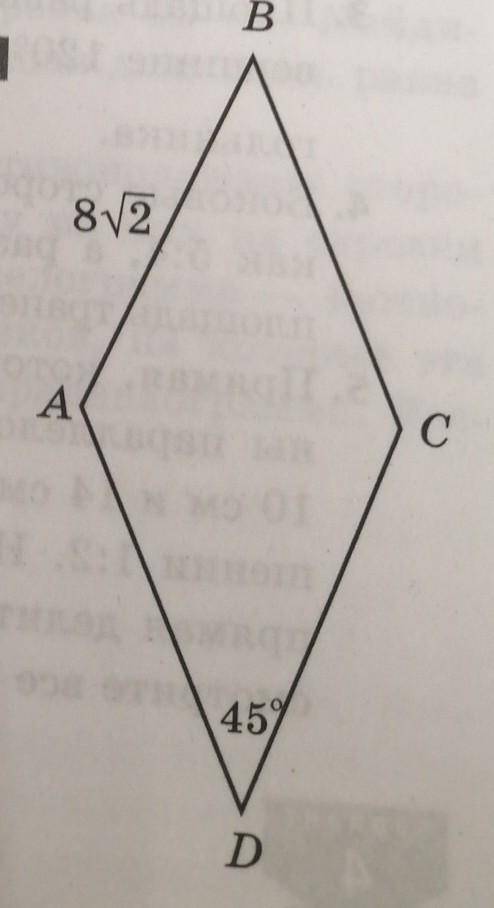
На рисунке ABCD ромб, угол D=45, AB=8 корень из 2. Найдите площадь

Для решения данной задачи, нам необходимо воспользоваться свойствами ромба.

Ромб имеет следующие свойства:
1. Все его стороны равны между собой.
2. Диагонали ромба перпендикулярны между собой и делят его на 4 равных треугольника.
3. Если в ромбе один из углов равен 45 градусам, то все углы ромба также равны 45 градусам.

Начнем с нахождения длины стороны ромба.
Мы знаем, что AB=8√2.
Угол D равен 45 градусам, а значит, угол ADC также равен 45 градусам.
Так как углы ACD и DCA равны, то треугольник ADC - равнобедренный прямоугольный треугольник.
Таким образом, по теореме Пифагора, мы можем найти длину диагонали AC:
AC = √(AD² + DC²) = √(8² + 8²) = 8√(2 + 1) = 8√3.

Так как AC является диагональю ромба, она делит его на 4 равных треугольника.
Значит, высота каждого треугольника будет равна половине длины диагонали AC:
h = AC/2 = (8√3)/2 = 4√3.

Теперь мы можем найти площадь каждого треугольника, используя формулу для площади прямоугольного треугольника:
S = (a * b)/2,
где a и b - длины катетов треугольника.

В нашем случае, основание треугольника равно длине стороны ромба AB, то есть 8√2, а высота равна 4√3.
Подставляем значения в формулу:
S = (8√2 * 4√3)/2 = 32√(2*3)/2 = 16√6.

Так как треугольников 4, то общая площадь ромба будет равна площади одного треугольника, умноженной на 4:
Площадь = 16√6 * 4 = 64√6.

Ответ: Площадь ромба ABCD равна 64√6.