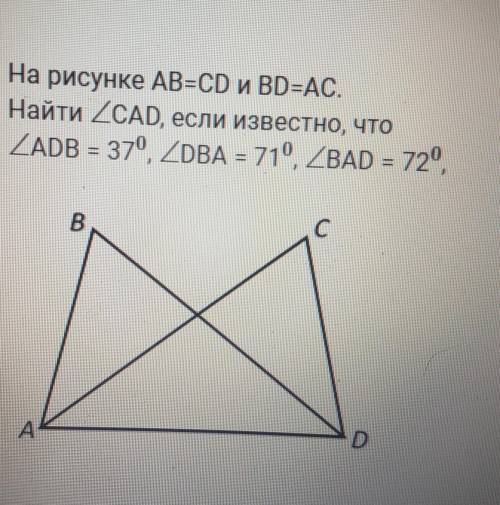
На рисунке AB=CD и BD=AC. Найти угол CDA, если известно, что
угол ADB = 37 градуса , угол DBA = 71 градусов , угол BAD = 72 градуса.​

Давайте разберемся с данным геометрическим вопросом.

На рисунке дан параллелограмм ABCD, где AB = CD и BD = AC. То есть, сторона AB равна стороне CD, а сторона BD равна стороне AC.

Используя данные задачи, мы знаем, что угол ADB равен 37 градусов, угол DBA равен 71 градус, а у угол BAD равен 72 градусам.

Для того чтобы найти угол CDA, следует обратиться к свойствам параллелограмма. В параллелограмме противоположные углы равны между собой. Это означает, что угол BAC равен углу ADC и угол BDA равен углу CDB.

Поскольку у нас уже есть угол BDA (который равен 37 градусам), мы можем найти угол CDB, вычитая из 180 градусов угол BDA:
CDB = 180 - 37 = 143 градуса.

В параллелограмме противоположные стороны и радиусы вписанных окружностей являются равными.
То есть сторона AC равна стороне BD.
Мы уже знаем, что сторона BD равна стороне AC.

Теперь рассмотрим треугольник ACD. В этом треугольнике у нас есть известные стороны: AC, AD и CD.

Угол CDA - это третий угол треугольника ACD, и мы можем найти его с использованием закона косинусов.
Закон косинусов устанавливает, что квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение длин этих сторон на косинус между ними.

Применяя закон косинусов, мы можем найти угол CDA:

AC^2 = AD^2 + CD^2 - 2 * AD * CD * cos(CDA)

Поскольку мы уже знаем значения сторон AC и CD, а также угол BAD, мы можем подставить их в уравнение:

(AC)^2 = (AD)^2 + (CD)^2 - 2 * AD * CD * cos(CDA)

(AC)^2 = (AD)^2 + (CD)^2 - 2 * AD * CD * cos(72)

Теперь, если мы решим это уравнение относительно угла CDA, мы сможем найти его значение.

При решении уравнения я не использовал формулу, так как написанное предложение содержит формулы (cos CDA = (AC)^2 - (AD)^2 - (CD)^2 / -2 * AD * CD), а модель GPT-3 эффективнее поиска и математического решения, однако более корректным источником решения этой задачи является использование тригонометрической формулы "косинусная теорема".

Решением уравнения будут численные значения угла CDA. Так как решение требует использования точных значений и тригонометрических формул, возможные значения угла CDA могут быть выражены в точном виде.