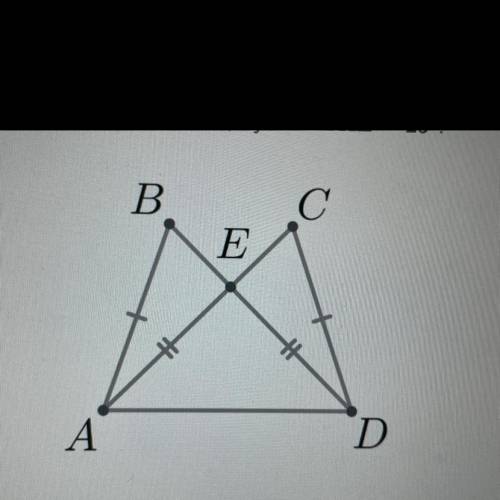
На рисунке AB = CD, AE = ED, AC = BD, a угол
Найдите угол

Дано, что AB = CD, AE = ED, AC = BD и изображен угол x.

Чтобы найти значение угла x, будем использовать информацию о равенстве сторон и выводить другие равенства углов.

1. Из равенства сторон AB = CD и AC = BD следует, что треугольники ABC и CBD равны по двум сторонам и углу при основании. Это следует из свойства равенства треугольников SSS (сторона-сторона-сторона). Обозначим углы в треугольнике ABC как углы A, B и C, а углы в треугольнике CBD как углы C, B и D.

2. Из равенства AE = ED следует, что углы AED и EDA равны, так как это свойство равенства сторон. Обозначим угол AED как угол a.

3. Так как внутри треугольника сумма углов равна 180 градусов, угол B в треугольнике ABC равен 180 - угол A - угол C.

4. Так как треугольники ABC и CBD равны, углы A и C в треугольнике ABC равны углам C и B соответственно в треугольнике CBD.

5. Обозначим угол B в треугольнике CBD как угол b, тогда угол C в треугольнике ABC также будет равен углу b.

Теперь у нас есть следующая информация:
- Углы A и C в треугольнике ABC равны углам C и B в треугольнике CBD.
- Углы B и C в треугольнике ABC в сумме дают 180 градусов.

Теперь рассмотрим угол x на рисунке и его расположение относительно треугольников ABC и CBD.

- Угол x является вертикальной противоположностью угла C в треугольнике ABC (по дополняющей теореме углов).
- Угол x является вертикальной противоположностью угла B в треугольнике CBD (так как они вершины одного угла).
- Углы B и C в сумме дают 180 градусов, поэтому x + B + C = 180.

Теперь мы можем записать следующие уравнения:
x + B + C = 180 (1)
A + C = C + B (2)

Так как A + C = C + B, то угол A также равен углу B. Заменим углы B на A в уравнении (1):
x + A + C = 180

Из свойства равенства углов мы можем переставить слагаемые:
x + C + A = 180

Также мы помним, что A + C = C + B, поэтому можем заменить C + B на A + C:
x + (C + B) = 180

C + B в скобках равно (A + C), поэтому можем заменить скобки:
x + (A + C) = 180

A + C в скобках равно (A + C), поэтому можем заменить скобки:
x + (A + C) = 180

Так как A + C = A + C, то угол x может быть любым значением, так как он не зависит от других углов и сторон треугольника.

Вывод: Угол x может иметь любое значение и мы не можем однозначно его определить только по заданным равенствам сторон и углов.