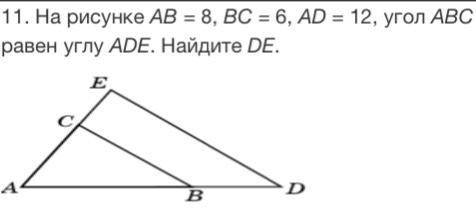
На рисунке AB = 8, BC = 6, AD = 12, угол ABC равен углу ADE. Найдите DE.

Для решения этой задачи мы можем воспользоваться свойствами треугольников и соответствующими углами. Дано: AB = 8, BC = 6, AD = 12, угол ABC равен углу ADE. Мы можем заметить, что у нас есть два треугольника: ABC и ADE. У этих треугольников есть несколько соотношений: 1. Треугольник ABC и треугольник ADE имеют одинаковую меру угла ABC и ADE, поэтому эти углы равны: ∠ABC = ∠ADE. 2. Треугольники ABC и ADE также имеют общую сторону AB и AC соответственно, и сторона BC || DE (параллельна). Из этого следует, что эти треугольники подобны: ΔABC ∼ ΔADE. Это означает, что соответствующие стороны этих треугольников пропорциональны. Теперь мы можем приступить к нахождению значения DE: Используем соответствующие стороны треугольников ABC и ADE. Следуя пропорции, получаем: AB/AD = BC/DE. Подставляем известные значения: 8/12 = 6/DE. Упрощаем пропорцию: 2/3 = 6/DE. Далее, мы можем решить эту пропорцию, умножив обе части на DE: (2/3)DE = 6. Избавляемся от дроби, умножая обе части на 3/2: DE = (6)(3/2). DE = 18/2. DE = 9. Итак, мы нашли, что DE = 9.