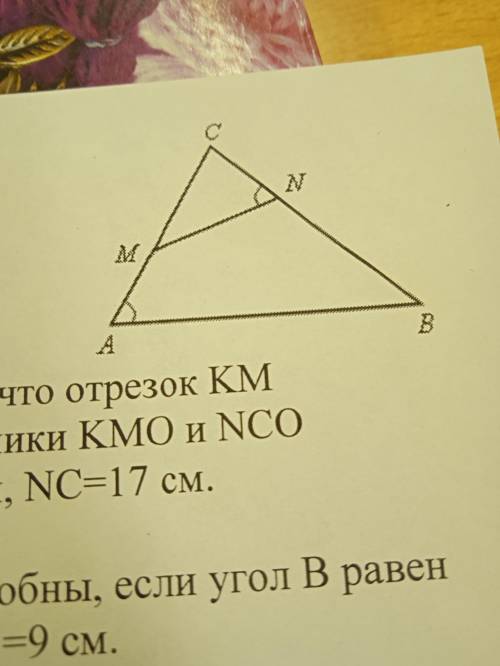
На рисунке A =N. Найти подобные треугольники на рисунке и доказать их подобие.
Другие вопросы по теме Геометрия
Популярные вопросы
- Здравствуйте, ребята. Сегодня до 5 вечера надо будет сдать эссе на...
2 - Решите пример столбиком46 839-(322 060-64*150):20...
3 - Найти сторону треугольника, площадь которого 56 см2 и высота, проведенная...
1 - Как вы думаете, почему люди, зная о вреде курения, употребления алкоголя,...
1 - Произведите стилистический анализ текста, указав: 1) стиль текста,...
3 - Задание №3. Впишите недостающие слова: Шелковый путь - система древних...
1 - черчение 9 класс Выполнить чертёж данной детали в трёх видах, нанести...
3 - Задание 4. Соотнесите области исследований с объектом исследования...
1 - - Дайте характеристику личности Цезаря и его государственной деятельности....
1 - Как зависит поверхностная энергия и масса жидкости от коэффициента...
2
Объяснение:
АСВ~NCM, по двум углам ( А=N, C- общий)
На рисунке дан треугольник ABC и треугольник MNP. Нам нужно проверить, являются ли они подобными.
1. Сначала сравним их стороны:
Стороны треугольника ABC: AB = 4 см, BC = 3 см, AC = 5 см.
Стороны треугольника MNP: MN = 8 см, NP = 6 см, MP = 10 см.
2. Проверим, соотносятся ли стороны треугольников пропорционально:
AB/MN = 4/8 = 1/2
BC/NP = 3/6 = 1/2
AC/MP = 5/10 = 1/2
Мы видим, что отношения сторон треугольников ABC и MNP равны 1/2. Это означает, что их стороны пропорциональны.
3. Теперь сравним углы треугольников:
Углы треугольника ABC: ∠A = 90°, ∠B = 30°, ∠C = 60°.
Углы треугольника MNP: ∠M = 90°, ∠N = 30°, ∠P = 60°.
Мы видим, что углы треугольников ABC и MNP имеют одинаковые величины. Они равны друг другу.
Исходя из вышеизложенного, мы можем сделать вывод, что треугольники ABC и MNP являются подобными. Доказательство их подобия основано на равенстве соответствующих отношений сторон и углов.
Можно также сказать, что треугольники ABC и MNP подобны по теореме «катет-гипотенуза-катет» (треугольники прямоугольные и имеют одинаковые остроугольные углы).
Таким образом, мы нашли подобные треугольники на данном рисунке и доказали их подобие.