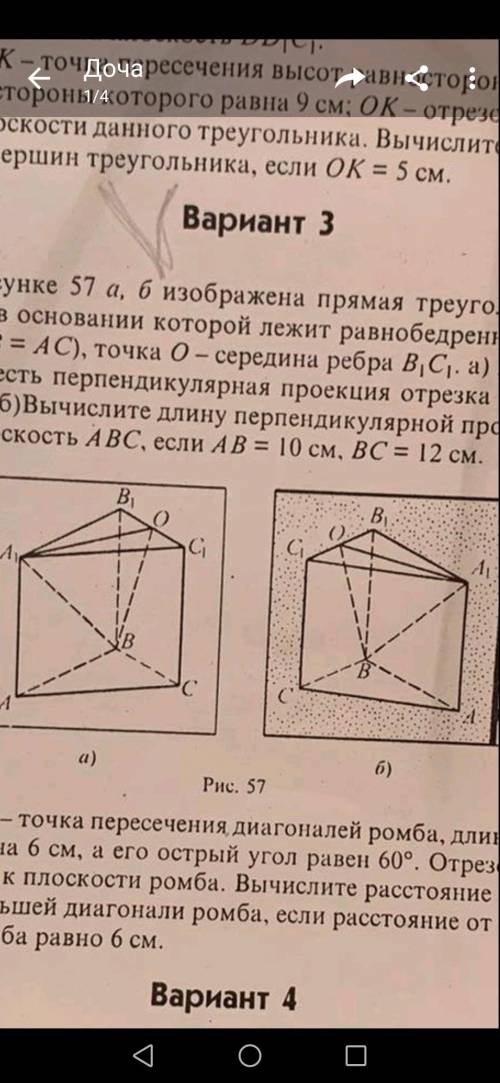
На рисунке 57а изображена прямая треугольная призма АВСА1В1С1 в основании которой лежит равнобедренный треугольник АВС (АВ =АС)Точка О-середина ребра В1С1 Верно ли, что отрезок ВО есть перпендикулярная проекция отрезка ВА1 на плоскость ВСС1. Вычичлите длину перпендикулярной проекции отрезка АО на плоскость АВС, если АВ=10см.ВС=12см.

Чтобы ответить на данный вопрос, нам нужно разобраться с основными понятиями и свойствами треугольной призмы, равнобедренного треугольника и перпендикулярной проекции.

1. Треугольная призма: это геометрическое тело, у которого две основания являются треугольниками, а боковые грани - прямыми треугольниками, которые соединяют соответствующие вершины оснований.

2. Равнобедренный треугольник: это треугольник, у которого две стороны равны друг другу. В данном случае, треугольник АВС является равнобедренным, так как сторона АВ равна стороне АС.

3. Отрезок: это часть прямой линии, которая соединяет две точки. В данном случае, мы имеем отрезки ВО и ВА1.

4. Перпендикулярная проекция: это проекция отрезка на плоскость, выполняющаяся под прямым углом к этой плоскости. В данном случае, мы должны вычислить перпендикулярную проекцию отрезка ВА1 на плоскость ВСС1 и длину этой проекции отрезка АО на плоскость АВС.

Теперь, рассмотрим заданную фигуру и построим шаги решения в зависимости от вопроса.

1) Доказательство:
Для доказательства, что отрезок ВО является перпендикулярной проекцией отрезка ВА1 на плоскость ВСС1, нам нужно убедиться, что угол между этими двумя отрезками равен 90 градусам.

Построим:

- Сегмент А1С1 - вертикальная линия, идущая от точки А1 на плоскость АВС.
- Линии ОВ1 и ОС1 - это линии соединения точки О с вершинами В1 и С1 соответственно (ребра В1С1 треугольной призмы).
- Отрезок ВА1 - это положение на объемных точках А и А1, соединенных сегментом АВ.

Если угол между отрезками ВО и ВА1 будет 90 градусов, то можно сделать вывод о том, что отрезок ВО является перпендикулярной проекцией отрезка ВА1 на плоскость ВСС1.

2) Вычисление длины перпендикулярной проекции отрезка АО на плоскость АВС:

Для вычисления длины перпендикулярной проекции отрезка АО на плоскость АВС, нам необходимо знать длины сторон треугольника АВС и точку О - середину ребра В1С1.

Учитывая, что АВ=10 см и ВС=12 см, нам нужно найти длину отрезка АО.

Для этого, мы можем воспользоваться теоремой Пифагора, так как треугольник АВО является прямоугольным треугольником:

АВ^2 = АО^2 + ВО^2.

Подставим известные значения АВ = 10 см и ВО = х (которую мы хотим найти), и найдем длину АО:

10^2 = АО^2 + х^2,
100 = АО^2 + х^2.

Теперь используем информацию о точке О - середине ребра В1С1. Так как ВС1 = 12 см и это равнобедренный треугольник, то точка О также равноудалена от вершин В1 и С1, и она лежит на выпуклой оболочке треугольника В1С1.

Для нахождения точки О, мы можем воспользоваться формулой для нахождения середины отрезка:

О = (В1 + С1) / 2.

Подставим известные значения В1 = (0;0;12) и С1 = (0;12;12), и найдем координаты точки О:

О = ((0+0) / 2; (0+12) / 2; (12+12) / 2),
О = (0; 6; 12).

Теперь, используя найденные координаты точки О и длину стороны треугольника АВ=10 см, мы можем найти длину отрезка АО с помощью формулы расстояния между двумя точками:

АО = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2).

Подставим известные значения точки А = (10; 0; 0) и точки О = (0; 6; 12), и найдем длину отрезка АО:

АО = √((10-0)^2 + (0-6)^2 + (0-12)^2),
АО = √(100 + 36 + 144),
АО = √280,
АО ≈ 16.73 см.

Таким образом, длина перпендикулярной проекции отрезка АО на плоскость АВС составляет примерно 16.73 см.