На рисунке 35 отрезки AB и CD имеют общую середину O. Докажите, что угол DAO = углу CBO
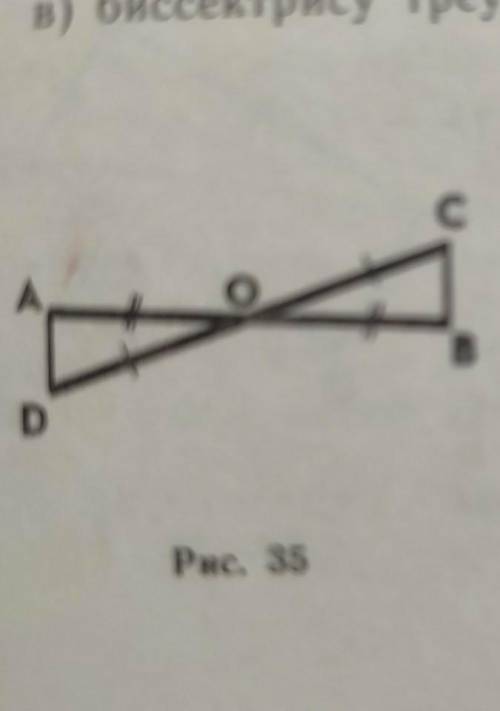
Другие вопросы по теме Геометрия
Популярные вопросы
- Колониальная политика европейских государств...
3 - «Весна народов» и эпоха консервативных реформ...
3 - В равнобедренном треугольнике основание в 2 раза меньше боковой...
2 - Причины революций XVII—XVIII вв. (Англия, Северная Америка и Франция)...
1 - Изменение отношений монарха и знати в Новое время...
2 - Эклектика - художественное направление и представители...
3 - Приведи факты, доказывающие ведущую роль машиностроения в экономике...
3 - Художественные течения второй половины XIX в. (сравнительная таблица)...
3 - Предпосылки стилевого разнообразия искусства второй половины XIX...
1 - Истоки и особенности стиля романтизм...
2
1. В задаче у нас имеется рисунок, на котором изображены отрезки AB и CD. Также на рисунке видно, что отрезки AB и CD имеют общую середину - точку O.
2. Чтобы доказать, что угол DAO равен углу CBO, нам необходимо знать, какие углы считаются равными. В математике, углы считаются равными, если у них равны меры. То есть, для доказательства, нам нужно показать, что меры угла DAO и угла CBO равны.
3. Рассмотрим треугольник ADO. Известно, что отрезок AO является медианой данного треугольника, и особенностью медианы является то, что она делит сторону пополам. То есть, отрезок AO делит сторону AD пополам. Аналогично, отрезок AO делит сторону DO пополам. Поэтому, точка O является серединой сторон AD.
4. Аналогично, рассмотрим треугольник BCO. Точка O также является серединой стороны BC.
5. Поскольку точка O является серединой сторон AD и BC, следовательно, сторона AD равна стороне OB, а сторона DO равна стороне OC. Это результат свойства медианы.
6. Теперь рассмотрим треугольники ADO и CBO. У них углы DAO и CBO взаимно соответственно равны, поскольку у них равны соответствующие стороны AD и OB, а также сторона DO равна стороне OC.
7. Таким образом, мы доказали, что угол DAO равен углу CBO.
Это - подробное решение задачи, которое можно дать школьнику, чтобы помочь ему понять задачу и способ ее решения. Надеюсь, я смогу помочь! Если у вас будут еще вопросы, не стесняйтесь задавать их.