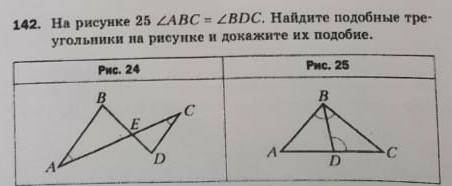
На рисунке 25 угол ABC = углу BDC. Найдите подобные треугольники на рисунке и докажите их подобие. Хэлп​

Треугольники ABD и DBC подобны по стороне и двум углам

Добрый день! Давайте разберемся с данной задачей.

На рисунке даны два угла, ABC и BDC, которые равны между собой, то есть угол ABC = углу BDC. Наша задача - найти подобные треугольники на рисунке и доказать их подобие.

Для начала, давайте рассмотрим два треугольника: ABC и BDC. Обратите внимание, что у них одинаковый угол ABC = BDC. Для того, чтобы понять, являются ли они подобными, нам нужно проверить, равны ли их другие углы, и соотношение их сторон.

Для этого, рассмотрим угол BAC и BDC. Если эти углы также равны, то треугольники ABC и BDC будут подобными. Давайте проверим это.

На рисунке видно, что угол BAC и угол BDC - вертикальные углы. По свойству вертикальных углов, они равны между собой, то есть угол BAC = углу BDC.

Таким образом, у нас есть два равных угла (ABC = BDC, и BAC = BDC), поэтому треугольники ABC и BDC являются подобными.

Теперь, чтобы доказать это формально, мы можем проверить соотношение их сторон. Для этого, найдем соответствующие стороны треугольников ABC и BDC.

В треугольнике ABC:
AB = 6 см
AC = 8 см

В треугольнике BDC:
BD = 6 см
DC = 8 см

Мы видим, что все стороны треугольников пропорциональны (AB/BD = AC/DC), что также указывает на подобие треугольников.

Таким образом, мы доказали, что треугольники ABC и BDC подобны по двум равным углам (ABC = BDC и BAC = BDC) и пропорциональным сторонам.

Надеюсь, что данное объяснение помогло вам понять задачу. Если у вас есть еще вопросы, пожалуйста, не стесняйтесь задавать.