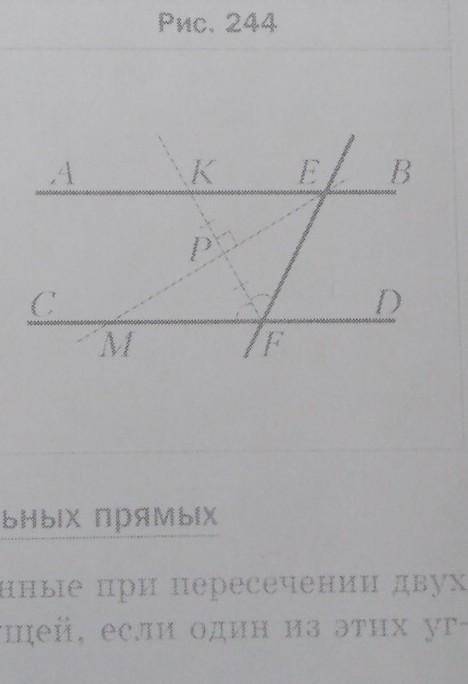
На рисунке 244 КР = FP, ∠MFK = ∠EFK, FK _I_ ME. Докажите, что прямые АВ и CD параллельны. На рисунке 244 КР = FP, ∠MFK = ∠EFK, FK _I_ ME. Докажите, что прямые АВ и CD параллельны​

Для доказательства параллельности прямых AB и CD на рисунке, нам понадобятся несколько геометрических фактов и результатов.

1. Факт 1: Если две прямые пересекаются с третьей прямой так, что сумма внутренних углов на одной стороне пересечения равна 180 градусов, то эти прямые параллельны.

2. Факт 2: Если две прямые пересекаются с третьей прямой так, что соответствующие углы (корреспонденты) равны, то эти прямые параллельны.

3. Факт 3: Если две прямые пересекаются с третьей прямой так, что внутренний угол на одной стороне пересечения равен наружному углу на другой стороне пересечения, то эти прямые параллельны.

Теперь, используя данные рисунка и эти факты, мы можем начать доказательство:

Дано:
На рисунке 244 KR = FP, ∠MFK = ∠EFK, FK || ME.

Цель:
Доказать, что AB || CD.

Доказательство:
1. Рассмотрим треугольники KRF и KME.
- Из условия, KR = FP и FK || ME.
- По факту 2, мы знаем, что если две прямые пересекают одну прямую так, что соответствующие углы равны, то эти прямые параллельны.
- Значит, треугольники KRF и KME подобны по факту 2.
- Значит, соответствующие стороны этих треугольников пропорциональны.

2. Рассмотрим треугольники KMF и KEF.
- Из условия, ∠MFK = ∠EFK.
- По факту 3, мы знаем, что если две прямые пересекают одну прямую так, что внутренний угол на одной стороне равен наружному углу другой стороны, то эти прямые параллельны.
- Значит, прямые MF и EF параллельны по факту 3.
- Значит, треугольники KMF и KEF подобны по факту 2.
- Значит, соответствующие стороны этих треугольников пропорциональны.

3. Из условия, KR = FP и пропорциональности сторон треугольников KRF и KME, мы можем заключить, что KF = ME.

4. Рассмотрим треугольники KAE и KFC.
- Из условия, ME || FK.
- По факту 2, мы знаем, что если две прямые пересекают одну прямую так, что соответствующие углы равны, то эти прямые параллельны.
- Значит, треугольники KAE и KFC подобны по факту 2.
- Значит, соответствующие стороны этих треугольников пропорциональны.

5. Из пропорциональности сторон треугольников KAE и KFC, а также равенства ME = FK, мы можем заключить, что AE = CF.

6. Итак, мы получили, что стороны AB и CD прямых, пересекающихся с третьей прямой (KF), пропорциональны друг другу (по пункту 3) и равны друг другу (по пункту 5).

7. Поэтому, сумма внутренних углов на одной стороне пересечения AB (углы KEF и KFC) равна 180 градусов (по свойству треугольника) и, следовательно, по факту 1, прямые AB и CD параллельны.

Таким образом, мы доказали, что прямые AB и CD параллельны, используя данные рисунка и факты 1-3.