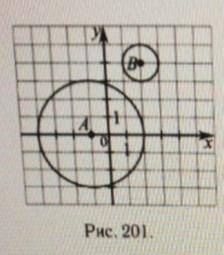
На рисунке 201 изображены окружности с центрами в точках А и В. Напишите их уравнения.

1) Самый короткий это, ломанная, состоящая из двух отрезков,: от А к С, затем от С к В

2) Прямые АС и СВ - радиусы, AC = 4, BC = 3, значит этот путь равен 4 + 3 = 7

Объяснение:///

Добрый день! Давайте разберем вместе это задание.

На рисунке 201 показаны две окружности с центрами в точках А и В. Чтобы найти уравнение окружности, нам понадобится уравнение окружности в общем виде:

(x - h)^2 + (y - k)^2 = r^2,

где (h, k) - координаты центра окружности, а r - радиус окружности.

У первой окружности центр находится в точке А, которая имеет координаты (2, -3). Радиус окружности можно определить, измерив расстояние от центра до любой точки на окружности. На рисунке нет отметок таких точек, поэтому мы не знаем радиус. Мы можем указать его с помощью переменной r, чтобы представить все возможные окружности с центром в точке А. Таким образом, уравнение окружности с центром в точке А будет иметь вид:

(x - 2)^2 + (y + 3)^2 = r^2.

Для второй окружности центр находится в точке В, которая имеет координаты (-4, 1). Аналогично первой окружности, мы не знаем радиус, поэтому будем использовать переменную r. Уравнение для второй окружности будет выглядеть следующим образом:

(x + 4)^2 + (y - 1)^2 = r^2.

Теперь у нас есть уравнения для обеих окружностей:
1) (x - 2)^2 + (y + 3)^2 = r^2,
2) (x + 4)^2 + (y - 1)^2 = r^2.

Надеюсь, я смог объяснить ответ на ваш вопрос достаточно подробно и понятно. Если у вас есть еще вопросы, не стесняйтесь задавать их!