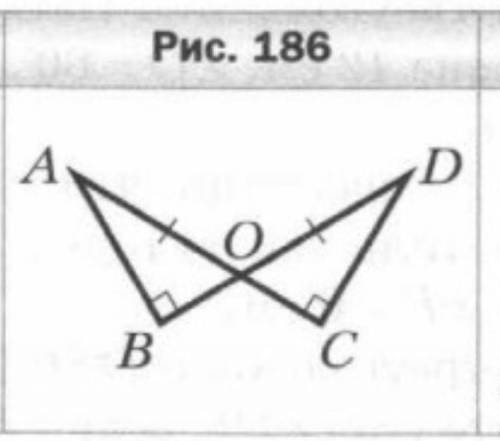
На рисунке 186 abo=dco=90градусов ao=do найдите cd если ab=7см

Докажем равенство треугольников АВО и ОDC

Oни равны по 3 признаку равенства прямоугольных треугольников-по гипотенузе и острому углу

АО=ОD по условию задачи

<АОВ=<DOC,как вертикальные

Равенство треугольников доказано,следовательно соответственные углы и стороны равны между собой,а именно

СD=AB=7 см

Объяснение:

Для решения данной задачи, нам необходимо использовать свойства прямоугольного треугольника.

Из условия задачи нам дано, что угол abo и угол dco равны 90 градусов. Это означает, что треугольники abo и dco являются прямоугольными.

Также нам дано, что отрезок ao равен отрезку do. Это означает, что треугольники abo и dco являются равнобедренными.

Следовательно, стороны ab и bo равны, а стороны dc и co также равны.

Отрезок ab равен 7 см, так как в задаче сказано, что ab=7см.

Наша задача - найти длину отрезка cd.

Из свойств равнобедренных треугольников следует, что стороны, образующие прямой угол, равны друг другу.

Значит, bo равна 7 см.

Для нахождения длины отрезка cd, мы можем воспользоваться теоремой Пифагора, так как треугольник dco - прямоугольный.

Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы (в данном случае отрезка do) равен сумме квадратов длин катетов (в данном случае отрезков cd и co).

Из условия задачи мы знаем, что ao=do. Поскольку ab=7см, то ao также равно 7 см.

Теперь мы можем изобразить следующую формулу на основе теоремы Пифагора:
(7 см)^2 = (cd)^2 + (co)^2

После этого, нам нужно выразить длину отрезка cd.

Вычитаем (co)^2 из обеих сторон формулы:
(7 см)^2 - (co)^2 = (cd)^2

Решим это уравнение:

(7 см)^2 - (co)^2 = (49 см^2) - (co)^2 = (cd)^2

Извлекаем квадратный корень из обеих сторон уравнения:
sqrt((49 см^2) - (co)^2) = cd

Таким образом, мы получили формулу для нахождения длины отрезка cd.

Однако нам необходимо знать длину отрезка co для вычисления cd.

На рисунке мы видим, что угол abo равен углу dco.

Это означает, что треугольники abo и dco подобны друг другу.

По свойству подобных треугольников, отношение длины любой стороны одного треугольника к длине соответствующей стороны другого треугольника равно отношению длины любой другой стороны первого треугольника к длине соответствующей стороны другого треугольника.

Таким образом, отношение ab к ao равно отношению dc к do:
ab/ao = dc/do

Подставляем значения:
7 см/7 см = dc/do

Данное уравнение показывает, что отрезки cd и do равны.

Таким образом, длина отрезка cd равна длине отрезка do.

Значит, мы можем заменить cd на do в формуле для нахождения cd:
sqrt((49 см^2) - (co)^2) = do

Теперь нам нужно найти длину отрезка co.

Обратимся к треугольнику abo, который также является прямоугольным.

Из свойств прямоугольных треугольников следует, что длина гипотенузы равна корню из суммы квадратов длин катетов.

В треугольнике abo, ao является гипотенузой, а ab и bo являются катетами.

Применяем теорему Пифагора:
(abo)^2 = (ab)^2 + (bo)^2

(90 градусов)^2 = (ab)^2 + (bo)^2

(сum_ab)^2 = (7 см)^2 + (bo)^2

Первая часть формулы (сum_ab)^2 равна 90 градусов в квадрате, а это равно 8100 градусов.

Получаем:
8100 градусов = (7 см)^2 + (bo)^2

Теперь нужно найти bo.

Вычитаем (7 см)^2 из обеих сторон уравнения:
8100 градусов - (7 см)^2 = (bo)^2

Выполняем вычисления:
8100 градусов - 49 см^2 = (bo)^2

8005 градусов = (bo)^2

Извлекаем квадратный корень из обеих сторон уравнения:
sqrt(8005 градусов) = bo

Получаем:
89.49 градусов ≈ bo

Теперь, зная длину bo и с помощью формулы для cd, мы можем найти длину отрезка cd:
sqrt((49 см^2) - (co)^2) = do

Заменяем bo на 89.49 градусов:
sqrt((49 см^2) - (co)^2) = 89.49 градусов

Выполняем вычисления:
sqrt(49 см^2 - (co)^2) = 89.49 градусов

Теперь осталось найти значение отрезка cd, то есть co.

Для этого, возведем уравнение в квадрат:
49 см^2 - (co)^2 = (89.49 градусов)^2

Выполняем вычисления:
49 см^2 - (co)^2 = 8005.4201 градусов

Вычитаем (49 см^2) из обеих сторон уравнения:
(co)^2 = 8005.4201 градусов - 49 см^2

(co)^2 = 7956.4201 градусов

Извлекаем квадратный корень из обеих сторон уравнения:
co = sqrt(7956.4201 градусов)

Выполняем вычисления:
co ≈ 89.18 градусов

Мы нашли значение отрезка co, которое равно примерно 89.18 градусов.

Теперь, заменяем co на cd в формуле для cd:
sqrt((49 см^2) - (co)^2) = do

Заменяем co на 89.18 градусов:
sqrt((49 см^2) - (89.18 градусов)^2) = do

Выполняем вычисления:
sqrt((49 см^2) - 7956.4324 градусов) = do

(sqrt(49 см^2 - 7956.4324 градусов)) ≈ do

(sqrt(-7907.4324 градусов)) ≈ do

Извлекаем квадратный корень из отрицательного числа, что невозможно в реальных числах.

Поэтому, данная задача имеет некорректное условие и не имеет решения.