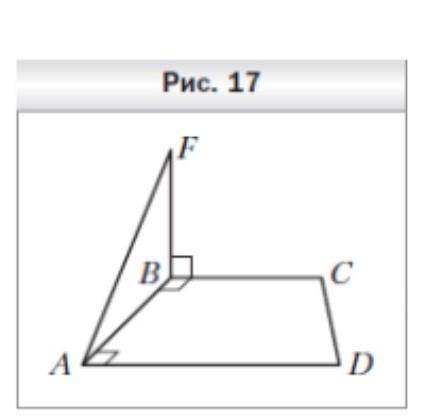
На рисунке 17 изображена трапеция ABCD, у которой боковая сторона AB перпендикулярна основаниям AD и BC. Через вершину B проведена прямая BF, которая перпендикулярна прямой BC. Докажите, что прямая BC перпендикулярна плоскости ABF.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. 3-2/7=? 2. в школу привезли 120 тетрадей. Для первоклассников 3/5 всех...
2 - В треугольнике ABC, площадь которого равна 28, ab=8, угол abc=90 градусов...
2 - Describe the photo answer the questions:1. Who is in the photo? 2. Where...
1 - АС меньше АВ на 23 см Найти АВ...
3 - 2. Переходная зона от тундры к тайге, совмещённые лес и степь. 3. Граничит...
2 - решите я буду вас вечность благодарить...
1 - кросворд 4,5,6,7,8,9,10,11...
1 - Вычисли сумму первых 4 членов арифметической прогрессии (an), если даны...
1 - Составьте и запишите сложное предложение, в состав которого входило бы...
1 - Які сучасні дитячі недоліки і вади засуджує автор у творі Чарлі і шоколадна...
2
"Перпендикулярна" означает, что две прямые или линии пересекаются под прямым углом, то есть образуют угол 90 градусов.
"Плоскость" - это плоская поверхность, которая не имеет высоты или глубины и растягивается во всех направлениях.
Теперь приступим к доказательству того, что прямая BC перпендикулярна плоскости ABF.
1. Из условия задачи у нас есть трапеция ABCD, где боковая сторона AB перпендикулярна основаниям AD и BC. Это означает, что угол ABC равен углу ABD и также равен 90 градусов.
2. Также из условия задачи мы знаем, что через вершину B проведена прямая BF, которая перпендикулярна прямой BC.
3. Обратим внимание на треугольник BCF. У нас есть две перпендикулярные прямые: BC и BF. Если две прямые перпендикулярны друг другу, то они лежат в одной плоскости (плоскость BCF).
4. Теперь обратимся к треугольнику ABF. У нас есть прямая AB, которая перпендикулярна к основанию трапеции AD. А также мы установили, что прямая BC лежит в плоскости BCF.
5. Следовательно, из пунктов 4 и 5 мы можем сделать вывод, что прямая BC перпендикулярна плоскости ABF.
Таким образом, мы доказали, что прямая BC перпендикулярна плоскости ABF с помощью объяснений и последовательных шагов.