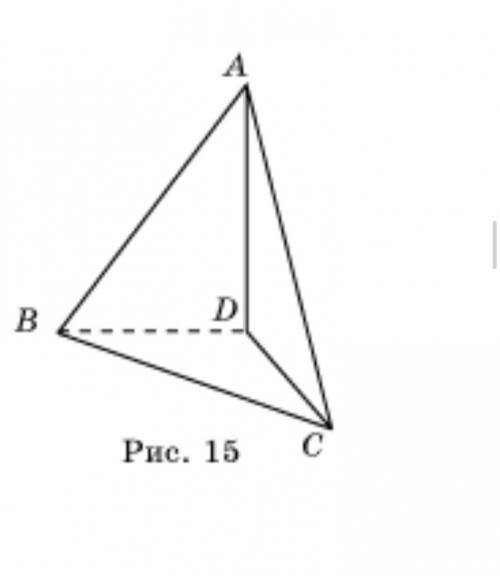
На рисунке 15 изображена пирамида ABCD, у которой углы ADB, ADC и BDC прямые. Найдите центр сферы, описанной около данной пирамиды.

1) Через середину гипотенузы строим прямую а, перпендикулярную основанию.

2) В плоскости, которая задается этой прямой и ребром AD проводим серединный перпендикуляр к AD.

3) Точка пересечения серединного перпендикуляра и прямой а - центр описанной сферы.

Объяснение:

Если сфера описана около данной пирамиды, то основание пирамиды вписано в окружность - сечение сферы.

Основание - прямоугольный треугольник. Центр описанной около него окружности лежит на середине гипотенузы.

Пусть Н - середина гипотенузы ВС прямоугольного треугольника BCD.

Тогда точка Н - центр окружности, описанной около ΔBCD,  равноудалена от всех вершин основания.

Проведем через точку Н прямую а║AD. AD⊥(BCD), так как AD⊥BD и AD⊥DC, значит а⊥(BCD).

Центр сферы будет лежать на прямой а.

Любая точка прямой а равноудалена от вершин основания. Осталось найти на ней точку, удаленную от вершины А на то же расстояние, что и от остальных вершин.

Для этого в плоскости (ADH) проведем серединный перпендикуляр к ребру AD. К - середина AD, проведем КО║DН до пересечения с прямой а.

О - центр сферы.