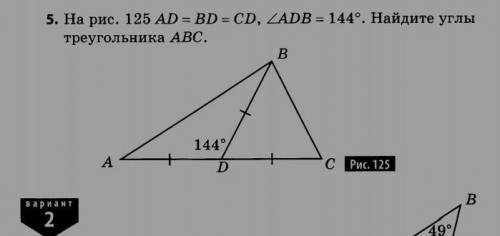
На рисунке 135 AD равно BC BD равно CD угол ADB равно 144 градуса Найдите углы треугольника ABC​

Для решения данной задачи нам нужно найти углы треугольника ABC, используя информацию, которая дана на рисунке.

Сначала обратим внимание на длины сторон треугольника. По условию, AD равно BC и BD равно CD. Это означает, что треугольник ABC является равнобедренным, так как две его стороны равны.

Теперь посмотрим на угол ADB, который равен 144 градуса. Для нахождения остальных углов треугольника ABC, нам нужно воспользоваться свойством суммы углов треугольника.

Сумма углов треугольника равна 180 градусам. Обозначим угол BAC как x, угол ABC как y, а угол ACB как z. Тогда можем записать следующее уравнение:

x + y + z = 180

Так как треугольник ABC равнобедренный, то углы BAC и BCA равны. Обозначим их как a. Тогда имеем следующее:

x = a
y = a
z = 180 - 2a

Теперь подставим полученные значения углов в уравнение:

a + a + 180 - 2a = 180

Сократим подобные слагаемые:

2a - 2a + 180 = 180

Остается:

180 = 180

Это равенство верно для любого значения а. Это означает, что треугольник ABC может быть любым равнобедренным треугольником, при условии, что его углы BAC и BCA одинаковы.

Итак, мы не можем точно определить углы треугольника ABC по данным условиям. Мы можем только сказать, что углы BAC и BCA равны друг другу, а сумма всех углов треугольника равна 180 градусам.