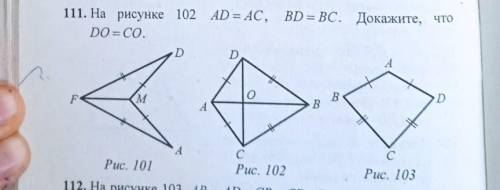
На рисунке 102 АД=АС ВД=ВС Докажите что ДО=СО​

Для доказательства того, что ОР = СР, мы можем воспользоваться двумя теоремами: теоремой о средней линии треугольника и теоремой о равнобедренности треугольника.

1. По теореме о средней линии треугольника, если точка M - середина стороны AB треугольника ABC, то длина отрезка BM равна половине длины стороны AC. То есть, BM = 1/2 * AC.

2. По теореме о равнобедренности треугольника, если в треугольнике две стороны равны, то два соответствующих угла при этих сторонах также равны. То есть, если AD = AC и VD = VC, то угол A также равен углу C, и угол D равен углу V.

Теперь, посмотрим на треугольник ABC на рисунке 102:

У нас имеются следующие равенства:
AD = AC (дано)
VD = VC (дано)
У нас также есть следующие равенства по двум теоремам:
AM = MC (по теореме о средней линии треугольника)
VM = MV (по теореме о средней линии треугольника)

Мы знаем, что OD = AM + MV (по определению суммы отрезков), а OC = MC + VM (по определению суммы отрезков).

Теперь применим наши равенства:
OD = AM + MV = MC + VM = OC.

Таким образом, мы доказали, что OD = OC и ОР = СР.