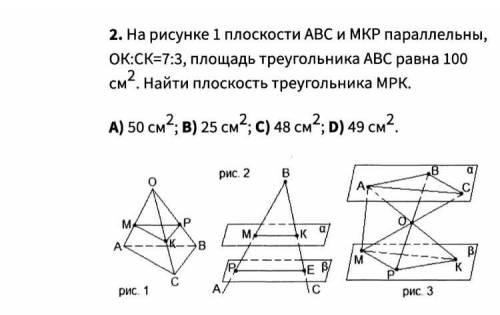
На рисунке 1 плоскости АВС и МКР параллельны, ОК:СК=7:3, площадь треугольника АВС равна 100 см2. Найти плоскость треугольника МРК.

Для решения этой задачи, нам необходимо использовать два свойства параллельных плоскостей и свойство подобных треугольников.

1. Свойство 1: Если две плоскости параллельны и прямая пересекает одну из них, то она пересекает и другую плоскость.

Из этого свойства следует, что прямая МК пересекает плоскость АВС.

2. Свойство 2: Если две плоскости параллельны и прямая пересекает одну из них, то пропорции длин отрезков, образованных пересечением прямой с обеими плоскостями, равны.

Из этого свойства следует, что ОК:СК = АК:БК = МК:КС.

Исходя из данного свойства, мы можем записать следующее уравнение:
7:3 = 70:КС.

Из этого уравнения можно найти значение КС:
7/3 = 70/КС.

Перекрестное умножение:
7КС = 210.

Развиваем:
КС = 210/7.

КС = 30.

Теперь мы знаем, что КС равно 30.

3. Свойство подобных треугольников: Если два треугольника подобны, то отношение площадей этих треугольников равно квадрату отношения их соответствующих сторон.

Используя это свойство, можем записать следующее равенство:
площадь треугольника АВС / площадь треугольника МРК = (АК:МК)^2.

Вставляем известные значения:
100 / площадь треугольника МРК = (70/30)^2.

Раскрываем скобки:
100 / площадь треугольника МРК = (7/3)^2.

Вычисляем квадрат:
100 / площадь треугольника МРК = 49/9.

Перекрестное умножение:
Площадь треугольника МРК * 49/9 = 100.

Разбиваем уравнение на две части:
Площадь треугольника МРК * 49 = 900.

Делим обе стороны на 49:
Площадь треугольника МРК = 900 / 49.

Вычисляем:
Площадь треугольника МРК ≈ 18.37 см².

Таким образом, площадь треугольника МРК составляет около 18.37 см².