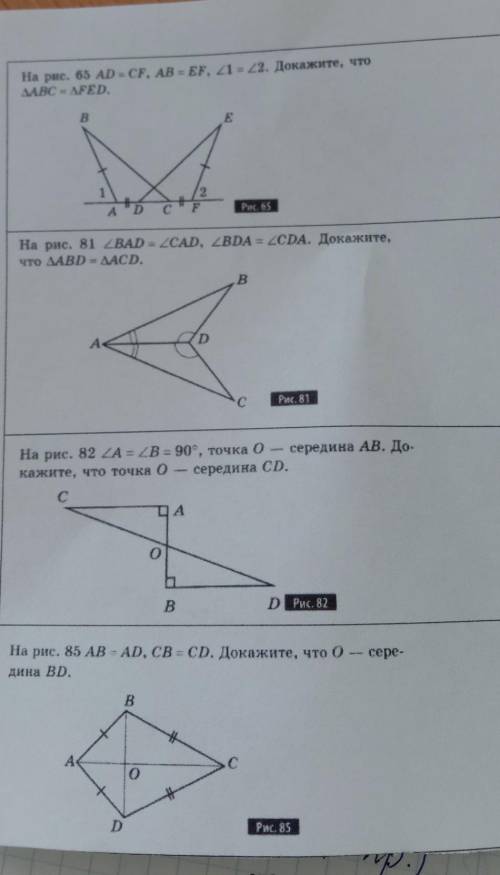
На рис.65 дано AD=CF, AB=EF, улг1=угл2 доказать: ΔABC=ΔFED
Другие вопросы по теме Геометрия
Популярные вопросы
- Put the words into the correct order 1.from/come/he/where 2. your/an/father/does/office/work/in...
3 - Синтексичний розбір речення соняшники- мов кулі жовтого вогню, їхнім...
2 - 1.на каком расстоянии от поверхности земли ускорение свободного...
3 - 5предложений научного стиля речи . и не копированный с интернета...
2 - Знайдіть складні речення,підкресліть у них граматичні основи.я дуже...
3 - Находить процентного отношения двух чисел 5 кг-100 кг= 6 тонна -...
3 - Как бы озоглавить отрывок из и всомнил олег коня своего...
3 - 100 б, (подробно решить) автомобиль “жигули» на скорости v = 50...
3 - Распредели словосочетания по таблице. узнать новое друзья договорились...
3 - Составить уравнение между хлоридом и фосфатом...
1
По условию задачи, у нас имеется:
AD = CF (дано)
AB = EF (дано)
угл1 = угл2 (дано)
Давайте рассмотрим каждое из этих равенств по отдельности:
1. AD = CF:
Это значит, что отрезок AD равен отрезку CF. Мы можем использовать это равенство, чтобы найти равные стороны в треугольниках ΔABC и ΔFED.
2. AB = EF:
Аналогично, это означает, что отрезок AB равен отрезку EF. Мы также можем использовать это равенство, чтобы найти равные стороны.
3. угл1 = угл2:
Это означает, что угол 1 равен углу 2. Мы можем использовать это равенство, чтобы найти равные углы в треугольниках.
Теперь давайте посмотрим, как применить эти равенства, чтобы установить равенство треугольников ΔABC и ΔFED:
1. Найдем равные стороны:
Из равенства AD = CF мы можем сказать, что сторона AD треугольника ΔABC равна стороне CF треугольника ΔFED.
Также из равенства AB = EF мы можем сказать, что сторона AB треугольника ΔABC равна стороне EF треугольника ΔFED.
Теперь у нас есть две пары равных сторон: AD равно CF и AB равно EF.
2. Найдем равные углы:
Из равенства угл1 = угл2 мы можем сказать, что угол 1 треугольника ΔABC равен углу 2 треугольника ΔFED.
У нас есть одна пара равных углов: угол 1 равен углу 2.
Теперь мы имеем равные стороны и равные углы в обоих треугольниках ΔABC и ΔFED. Согласно аксиоме о равенстве треугольников (ССС), если у двух треугольников стороны и углы одинаковы, то треугольники сами являются равными.
Таким образом, мы можем утверждать, что ΔABC = ΔFED, основываясь на равных сторонах и равных углах.