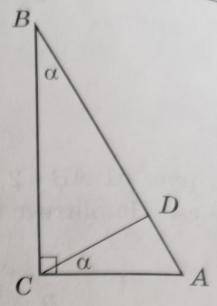
На рис. 64 ∠ACB = 90°, ∠B = ∠ACD = а. Назовите треугольники, подобные треугольнику ABC, и докажите их подобие.

На рисунке 64 дан треугольник ABC, в котором угол ACB равен 90°. Также известно, что угол B равен углу ACD и обозначен буквой "а".
Чтобы найти треугольники, подобные треугольнику ABC, мы должны найти другие треугольники, которые имеют с ним одинаковые углы. В данном случае, углы ACB и CDA равны 90°, а углы ABC и CAD равны "а".

1) Первый треугольник, подобный треугольнику ABC, - это треугольник CDA. Он имеет прямой угол у основания DA (как и угол ACB у треугольника ABC), и угол CDA равен "а" (как и угол B у треугольника ABC). Таким образом, углы треугольника CDA соответствуют углам треугольника ABC, и эти треугольники подобны.

Доказательство подобия треугольников ABC и CDA:
В треугольнике ABC и треугольнике CDA:
- Угол ACB и угол CDA равны 90° (одинаковые прямые углы).
- Угол ABC и угол CAD равны "а" (по условию).
- Угол BAC и угол CDA равны 180° - 90° - "а" = 90° - "а" (сумма углов треугольника равна 180°).

Таким образом, по теореме угловой подобности треугольников, треугольники ABC и CDA подобны.

2) Второй треугольник, подобный треугольнику ABC, - это треугольник CAB. Он имеет прямой угол у основания AB (как и угол ACB у треугольника ABC), и угол CAB равен "а" (как и угол B у треугольника ABC). Таким образом, углы треугольника CAB соответствуют углам треугольника ABC, и эти треугольники подобны.

Доказательство подобия треугольников ABC и CAB:
В треугольнике ABC и треугольнике CAB:
- Угол ACB и угол CAB равны 90° (одинаковые прямые углы).
- Угол ABC и угол BAC равны "а" (по условию).
- Угол BCA и угол CAB равны 180° - 90° - "а" = 90° - "а" (сумма углов треугольника равна 180°).

Таким образом, по теореме угловой подобности треугольников, треугольники ABC и CAB подобны.

Таким образом, мы доказали, что треугольники CDA и CAB подобны треугольнику ABC по двум углам.