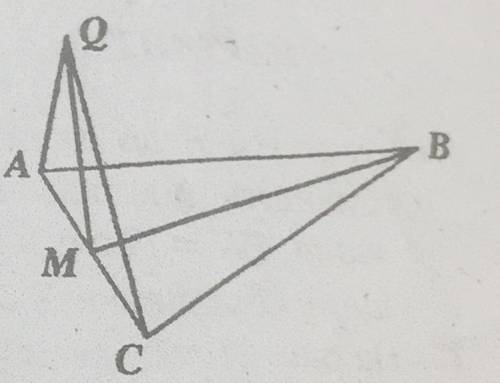
На рис. 19 изображено равнобедренный треугольник ABC (AB = BC), M - середина стороны AC. Через точку M проведена прямая MQ, перпендикулярной прямой BM. Докажите, что прямая BM перпендикулярна к плоскости AQC.
Другие вопросы по теме Геометрия
Популярные вопросы
- В каких ситуациях пешеходы обязаны иметь световозвращающие элементы?...
3 - С одного участка собрали 140 кг огурцов, а с другого в 3 раза больше....
1 - Сколько Метров(Куб) в 12434Км(Квадратных)...
2 - Суміжні кути мають однакову градусну міру...
1 - А Мәтіннен лингвистикалық терминдерді тауып,оларға морфологиялық талдау...
1 - ИССЛЕДОВАНИЕ ПРОЦЕССОВ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ Опыт 1. Исследование...
1 - Чему равны стороны прямоугольника, если его периметр равен 30 см, а...
2 - таблиця нужно здать завтра.Ето .Бо по литературе не шарю от слова нечего.✨...
3 - Сүйінбай мен Қатаған айтысына қандай жағдай түрткі болды? Айтыста Сүйінбай...
1 - ответьте на дополнительные вопросы к опыту. I. Какие кислоты образуют...
2
решение смотри на фотографии
Объяснение:
М- середина АС, значит, ВМ- медиана ΔАВС, но она проведена к основанию АС равнобедренного треугольника АВС, значит, является и высотой, т.е. ВМ⊥АС, по условию МQ⊥ВМ.
Значит, прямая ВМ перпендикулярна двум пересекающимся прямым плоскости АQC, конкретнее, MQ и AС,
и по признаку перпендикулярности прямой и плоскости, т.е.
если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
ВЫВОД. ВМ⊥ (АQC), доказано.