1. Геометрия
  2. на основании ас треугольника

на основании ас треугольника абс взяли точку е. отрезок бе пересекает среднюю линию мк треугольника в точке о.


на основании ас треугольника абс взяли точку е. отрезок бе пересекает среднюю линию мк треугольника

juwal juwal    2   07.02.2022 05:28    38

Ответы
Зозяська Зозяська  07.02.2022 06:00

Площадь трапеции ЕОКС равна 4S - S = 3S.

Это по условию, что площадь пропорциональна квадрату сходственных сторон: ЕС = 2ОК.

Так как АМОЕ и ЕОКС имеют одинаковую высоту, то отношение их площадей, равное 1/3, будет соответствовать и отношению сторон АЕ и ЕС.

ответ: АЕ/ЕС = 1/3.


на основании ас треугольника абс взяли точку е. отрезок бе пересекает среднюю линию мк треугольника
ПОКАЗАТЬ ОТВЕТЫ
george39 george39  07.02.2022 06:00

(см. объяснение)

Объяснение:

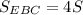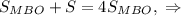
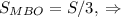
Из подобия треугольников EBC и OBK (1-ый признак) следует, что S_{EBC}=4S. Опять же, из того, что треугольники ABE и MBO подобны получаем 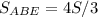S_{MBO}+S=4S_{MBO},\;\Rightarrow\;S_{MBO}=S/3,\;\Rightarrow\;S_{ABE}=4S/3. Опустим из вершины B высоту на AC. Тогда она будет общей для треугольников ABE и CBE.

Составим систему из формул их площадей:

\div \left\{\begin{array}{c}4S=\dfrac{1}{2}\cdot EC\cdot hdfrac{4S}{3}=\dfrac{1}{2}\cdot AE\cdot h\end{array}\right;

\dfrac{EC}{AE}=3,\;\Rightarrow\;EC:AE=3:1

Задание выполнено!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
tonkikhliza tonkikhliza  10.12.2020 20:48
1.     В системе координат нарисуй треугольник ABC с координатами вершин: A(−1;−1), B(−4,9;−1), C(−1;−4,9). 1)    Нарисуй треугольник A1B1C1, симметричный относительно...
meladse1105 meladse1105  10.12.2020 20:49
4. Вертикальная башня видна из точки К на поверхности земли под углом 600 Найдите высоту башни и расстояния от точки К до основания башни, если расстояние от точки К...
kolyakuzmin2006 kolyakuzmin2006  10.12.2020 20:50
2. Наблюдатель, который находится в точке А, ВИдит конец жерди Ви верхнюю точку башни D, причем точки A, B и D расположены на одной прямой. Определите высоту башни,...
Стихит Стихит  10.12.2020 20:50
УМОЛЯЮ ОТ Дан прямоугольный треугольник РQR с прямым углом R. Установите соответствия между отношениями сторон и тригонометрическими функциями острого угла: а) PRPQ;...
shabdanova16 shabdanova16  10.12.2020 20:51
На рисунке ∠OAC=∠OCA, ∠AOB=∠COB. Докажи, что △AOB=△COB....
Artem152006 Artem152006  10.12.2020 20:52
В треугольнике DEF /_D=/_F,DC=CE, FC ,CD=3,6см, EFбиссектриса. Найдите EF...
andrey4565178 andrey4565178  11.02.2021 11:17
Через вершини А і В трикутника АВС проведено коло, яке перетинає сторони AC і ВС у точках DiE відповідно. Відомо, що AB = 16 см, ВС = 12 см, CD - 3 см. Знайдіть відрізок​...
asia1406 asia1406  11.02.2021 11:16
Найдите площадь ромба если его высота равна 4,а острый угол равен 60 градусам​...
everlast112 everlast112  11.02.2021 11:12
В трапеции ABCD ∠A = 90°, АС = 6√2, ВС = 6, DE — высота треугольника ACD, a tg∠ACD = 2. Найдите СЕ скорее и с решением:3​...
mkim7119 mkim7119  28.05.2021 07:34
На рисунку АС=АК, В паралельно АС, CD паралельно АК. Доведіть, що СD=ВК​...

Популярные вопросы