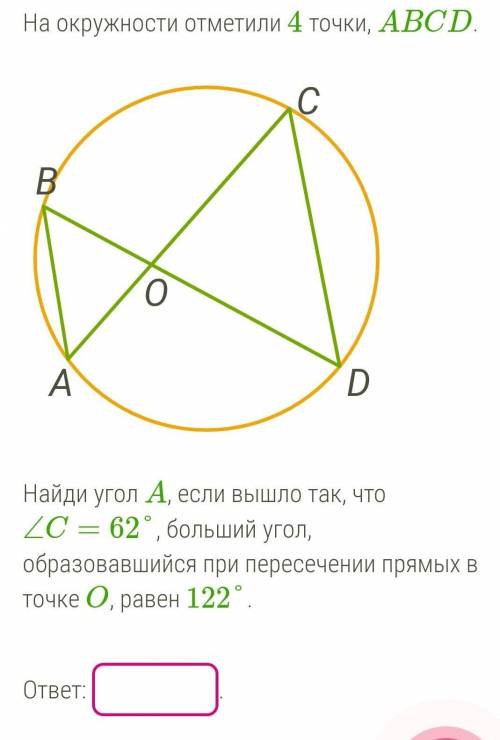
На окружности отметили 4 точки, ABCD. Найди угол A, если вышло так, что ∠C=62°, больший угол, образовавшийся при пересечении прямых в точке O, равен 122°​

Чтобы найти угол A, нам понадобится использовать свойства окружности и треугольника.

1. Вспомним свойства углов, образованных на окружности:

- Центральный угол, образованный любыми двумя радиусами, равен углу, стирающему соответствующую дугу на окружности. В данном случае угол COB равен углу на дуге CD.

- Угол, образованный хордой и соответствующей дугой, равен половине центрального угла. В данном случае угол COB равен половине угла A.

2. Теперь обратимся к треугольнику ABC и свойству углов треугольника:

- Сумма углов треугольника равна 180°. В данном случае угол А + угол В + угол C = 180°.

3. С учетом этих свойств, мы можем составить уравнение:

угол А + угол COB + угол C = 180°

угол А + 122° + 62° = 180°

угол А = 180° - 122° - 62°

угол А = 180° - 184°

угол А = -4°

Таким образом, получаем, что угол A равен -4°.