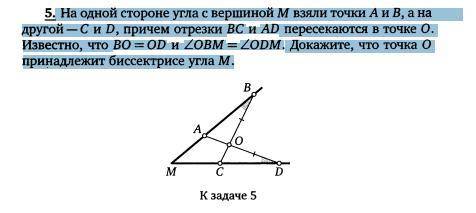
На одной стороне угла с вершиной М взяли точки Л и Б, а на другой —С и D, причем отрезки ВС и AD пересекаются в точке О. Известно, что ВО = OD и ZOBM = ZODM. Докажите, что точка О принадлежит биссектрисе угла М. Z-это угол
Другие вопросы по теме Геометрия
Популярные вопросы
- Какая соль na2hpo4 кислая или основная,двойная,смешанная, или комлексная...
2 - Синтаксический разбор предложения: неожиданно он вышел к огромной лесной...
1 - Придумать сказку про не существующую букву 1 класс....
3 - Составить предложения по схемам ах! - -! ох! - ой,- -! ух,- -! эй,- -!...
1 - Вмагазинне было 280 кг пшена. за день продали две седьмых этого пшена . поставь...
1 - Как решить номер 547 (3) (5\6-5\2)*(7\8-1\2)*(-4)...
3 - Всвязи с чем у человека появляются изгибы позвоночника?...
2 - Загадка на казахском языке про слона...
2 - Ex. 5. circle the correct word or phrase: 1 elizabeth usually goes\ is usually...
2 - Вычислить приблизительно значение корня √25,16...
3
смотри док-во ниже
Объяснение:
ΔAOB = ΔCOD по двум углам и прилежащей к ним стороне
ВО = OD, ∠OBM = ∠ODM - по условию задачи, а ∠AOB = ∠COD как вертикальные при пересекающихся прямых AD и BC
Из равенства треугольников следует, что AO=OC
Так как AO=OC и ВО = OD, то точка О равноудалена от лучей BM и DM, а значит она лежит на биссектрисе MО и принадлежит ей. ЧТД