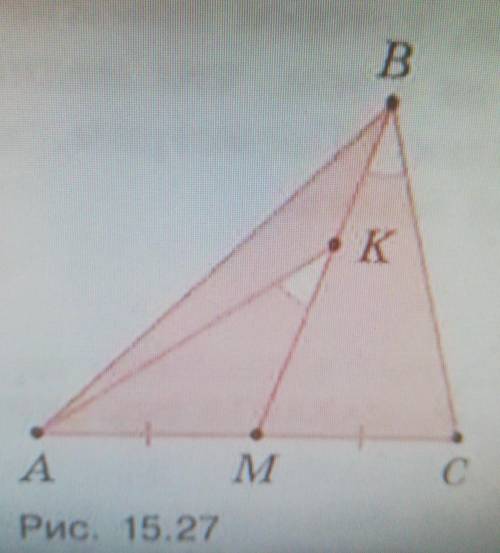
На медиане ВМ треугольника АВС взяли
точку K так, что угол AKM равен углу МВС.
Докажите, что отрезок АК равен одной из сторон
треугольника (рис. 15.27).​

Для начала, давайте разберемся с определениями, чтобы понять, что такое медиана и угол.

Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В данном случае медианой является отрезок ВМ.

Угол - это фигура, образованная двумя лучами, исходящими из одной точки. В данной задаче имеется несколько углов: угол AKM и угол МВС.

Теперь пошагово рассмотрим решение задачи:

Шаг 1: Допустим, что отрезок АК не равен ни одной из сторон треугольника.

Шаг 2: Угол AKM равен углу МВС (по условию задачи).

Шаг 3: Рассмотрим угол АКМ. Этот угол равен сумме углов АКС и угла МКС (по свойству угла). Обозначим угол АКС как α и угол МКС как β.

Шаг 4: Угол МВС также равен сумме углов МКС и угла МСВ (по свойству угла). Поскольку угол МКС равен углу АКМ, а угол МСВ является прямым углом (так как ВМ - медиана), то можно записать уравнение:

β + угол АКМ = угол МСВ.

Шаг 5: Исходя из равенства углов AKM и МВС, у нас получается следующее уравнение:

α + угол МСВ = β + угол АКМ.

Шаг 6: Поскольку треугольник АСМ является прямоугольным, то сумма углов его трех вершин равна 180 градусов. Мы можем записать следующее уравнение:

угол МСВ + угол АКМ + угол АКС = 180 градусов.

Шаг 7: Подставим значения из шагов 4, 5 и полученное уравнение из шага 6 в уравнение шага 5:

α + (β + угол АКМ) + угол АКС = 180 градусов.

Шаг 8: Упрощаем уравнение, объединяя похожие слагаемые:

α + β + угол АКМ + угол АКС = 180 градусов.

Шаг 9: Поскольку углы АКС и МКС равны, мы можем записать уравнение следующим образом:

α + β + 2 * угол АКМ = 180 градусов.

Шаг 10: Упрощаем уравнение:

2 * угол АКМ = 180 - α - β.

Шаг 11: Поскольку α и β являются фиксированными значениями (углы МКС и МСВ прямые), их сумма также является фиксированным значением. Таким образом, правая часть уравнения является постоянной величиной.

Шаг 12: Поскольку угол AKM равен углу МВС (по условию задачи), мы можем сделать вывод, что углы AKM и МКС также равны.

Шаг 13: Заменяем угол АКМ в уравнении шага 10 на угол МКС:

2 * угол МКС = 180 - α - β.

Шаг 14: Упрощаем уравнение:

угол МКС = (180 - α - β) / 2.

Шаг 15: Однако по условию задачи, мы знаем, что угол МВС равен углу AKM. Подставим это значение в уравнение:

угол МВС = (180 - α - β) / 2.

Шаг 16: Таким образом, поскольку углы МВС и МКС равны, мы получаем следующее равенство:

угол МВС = угол МКС.

Шаг 17: Заменяем уравнение шага 16 равенством из шага 15:

(180 - α - β) / 2 = угол МКС.

Шаг 18: Рассмотрим уравнение шага 9:

2 * угол АКМ = 180 - α - β.

Шаг 19: Поделим обе части уравнения шага 18 на 2:

угол АКМ = (180 - α - β) / 2.

Шаг 20: Таким образом, у нас получается следующее:

угол МКС = угол АКМ.

Шаг 21: Заменяем значение угла МКС из шага 14 на значение угла АКМ из шага 19:

угол МКС = (180 - α - β) / 2 = угол АКМ.

Шаг 22: Поскольку угол МКС и угол АКМ равны, это означает, что углы AKS и MSK также равны (так как они образованы одной вершиной и двумя пересекающимися лучами).

Шаг 23: Следовательно, отрезок АК параллелен отрезку МС.

Шаг 24: Поскольку отрезки АК и МС параллельны и имеют общую точку K, это означает, что АКМС представляет собой параллелограмм.

Шаг 25: В параллелограмме противоположные стороны и диагонали равны.

Шаг 26: Поскольку АК и МС являются противоположными сторонами АКМС, они должны быть равными.

Шаг 27: Таким образом, мы доказали, что отрезок АК равен одной из сторон треугольника АСВ.

Надеюсь, что это объяснение помогло понять решение задачи. Если у тебя есть еще вопросы или что-то не ясно, не стесняйся задавать.