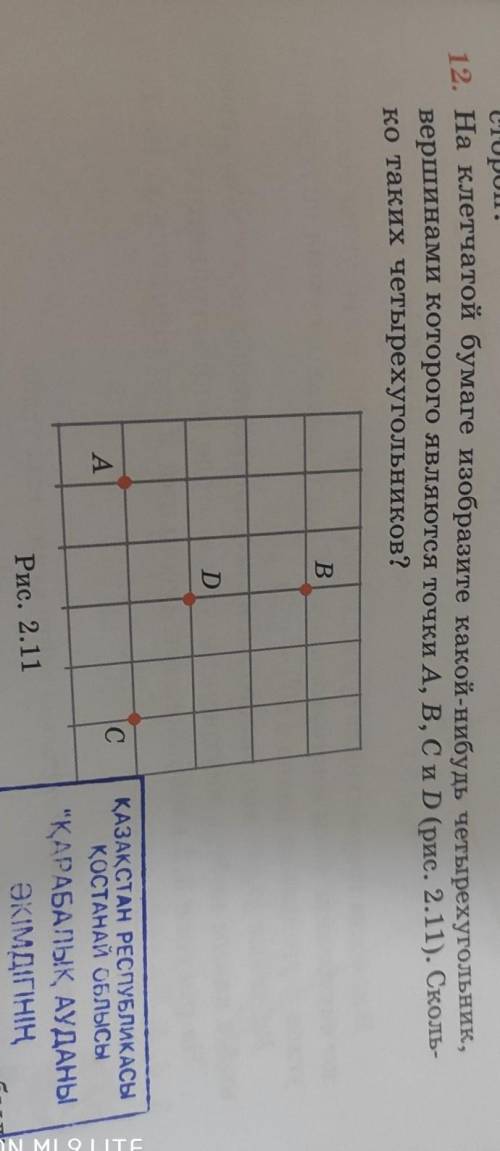
на клетчатой бумаге изобразите какой нибудь четырехугольник вершинами которого являются точки A B C и D (рис. 2.11) Сколько таких четырехугольников​

Для того чтобы нарисовать четырехугольник на клетчатой бумаге с вершинами A, B, C и D, нужно следовать следующим шагам:

1. На клетчатой бумаге нарисуйте оси координат, по которым можно будет определить положение вершин.
2. Затем нам нужно определить координаты каждой из вершин: A, B, C и D. На рисунке дана одна ось X и одна ось Y, поэтому мы можем использовать лишь две координаты для определения положения каждой точки.
3. Поскольку на рисунке нет никаких маркеров или измерений, мы можем только приближенно определить координаты вершин.
4. Например, можно предположить, что на рисунке расстояние между клетками на оси X и оси Y одинаково и равно единице. Поэтому, если мы предположим, что вершина A находится в точке (0,0), то мы можем приближенно определить координаты остальных вершин.
5. Взглянув на расположение точек B, C и D по отношению к A, мы можем сделать вывод о том, что вершина B находится в точке (1,2), вершина C в точке (3,4) и вершина D в точке (2,1).
6. Обратите внимание, что эти координаты приближенные и могут не быть абсолютно точными, так как изображение относительно маленькое и немасштабируемое.
7. Раз у нас есть координаты каждой вершины, мы можем соединить их, чтобы получить четырехугольник. Мы соединяем точку A с точкой B, затем точку B с точкой C, далее точку C с точкой D и, наконец, точку D с точкой A.
8. Когда соединение сделано, нарисуйте отрезки линий на клетчатой бумаге, чтобы показать четырехугольник.
9. Готово! Теперь у вас есть четырехугольник со своими вершинами A, B, C и D, изображенный на клетчатой бумаге.

Таким образом, на клетчатой бумаге можно изобразить несколько различных четырехугольников с вершинами A, B, C и D. Количество возможных четырехугольников зависит от того, насколько мы можем менять координаты вершин. В данном случае, если мы придерживаемся приближенных координат, то у нас только один вариант четырехугольника. Однако, если мы можем менять координаты вершин, количество возможных четырехугольников будет бесконечным.