На гранях пирамиды SJABCD провели медианы. Найдите расстояние между точками пересечения медиан соседних граней, если ребро тетраэдра равно 18: 1) 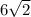
2) 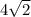
Другие вопросы по теме Геометрия
Популярные вопросы
- Составить предложения со словом кричат...
2 - Расставьте знаки препинания. она к моему удивлению принуждала меня...
1 - Найдите неизвестный член пропорции 0,25/2,8=0,75x...
1 - Треугольник abc равнобедренный сторона ac равна 36 мм, периметр-120мм....
2 - Составить предложение со словами. на кащакском языке таста.тастама.таза.лас.сақта...
2 - ответьте is it necessary to have work experience? is it easy to get...
2 - Е4упцауацуацка32й3к32222222222222222222...
2 - Здієсловами сушать, сушиш, сушимо склади й запиши речення....
3 - 1.возьмите груз массой 3-5 кг и держите его на вытянутой руке на уровне...
2 - Пример уравнения с дробями в три действия...
3
Давайте посмотрим на пирамиду SJABCD.
1) Первое, что мы должны сделать, это построить сечения плоскостями, параллельными граням SJAB и SADC. Пусть точка E - середина грани SJAB, а точка F - середина грани SADC.
Теперь нам нужно найти точку пересечения медианы грани JA с медианой грани DA. Пусть эта точка называется G.
Глядя на пирамиду, заметим, что точкой пересечения медиан граней JA и DA будет середина ребра JD. Обозначим эту точку как M. Теперь у нас есть плоскость, проходящая через точки E, F и M.
Таким образом, нам нужно найти расстояние между точками M и G. Поскольку M - это середина ребра JD, мы знаем, что M делит ребро JD пополам. Значит, расстояние от J до M будет равно половине длины ребра JD, то есть 18/2 = 9.
Чтобы найти расстояние от M до G, нам потребуется использовать теорему Пифагора. Мы видим, что треугольник JMG - прямоугольный треугольник, и с помощью теоремы Пифагора мы можем найти длину отрезка MG.
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В нашем случае MG - это гипотенуза, а JG и GM - это катеты.
Таким образом, у нас есть следующее уравнение: MG^2 = JG^2 + GM^2. Заменяя значения, которые мы знаем, получим: MG^2 = 9^2 + 6^2 = 81 + 36 = 117.
Чтобы найти MG, извлекаем квадратный корень из обеих сторон уравнения: MG = sqrt(117). Примерное значение этого корня равно 10,82.
Таким образом, расстояние между точками пересечения медиан соседних граней в данном случае равно примерно 10,82.
2) Для решения этого примера мы рассмотрим пирамиду SJABCD, аналогично первому примеру.
Мы знаем, что ребро тетраэдра составляет 18. Поэтому расстояние от вершины J до точки M, которая является серединой ребра JD, будет равно половине длины ребра JD, то есть 18/2 = 9.
Теперь мы можем использовать теорему Пифагора, чтобы найти расстояние между точками M и G, аналогично первому примеру. Теорема Пифагора даёт нам уравнение MG^2 = JG^2 + GM^2.
Подставляем известные значения: MG^2 = 9^2 + 6^2 = 81 + 36 = 117.
Извлекаем квадратный корень из обеих сторон уравнения: MG = sqrt(117). Примерное значение этого корня равно 10,82.
Таким образом, второй пример также дает нам расстояние между точками пересечения медиан соседних граней, равное примерно 10,82.