На эллипсе найти точку, для которой произведение фокальных радиус-векторов равно квадрату малой полуоси.
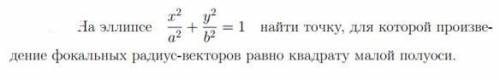
Другие вопросы по теме Геометрия
Популярные вопросы
- Можалуйста 1)вычеслите: a)6,73+15,658+3,27=? б)0,04*9,43*250=? 7 в)*18=? 9 2)решите...
3 - 10 класс.решите ,не понимаю: sinx -√3/2. заранее...
1 - Как самсон вырин воспитывал свою дочь?...
1 - Что из перечисленного относится к характеристике *культурной революции* в ? 1)демократицазция...
2 - Краткое сообщение на тему: много ли добра делают люди друг - другу с современном...
2 - Найдите в данных предложениях согласованные и несогласованные определения выпишите...
3 - Решите плз функцию желательно с пояснением...
2 - Сторона ромба дорівнює 13 см, а одна з діагоналей дорівнює 10 см . знайти другу...
1 - Ну и нормально а я думал что всё правильно...
2 - Запишите развернутую запись двоичного числа 110101...
2
Эллипс - это геометрическое место точек, для которых сумма расстояний до двух фокусов эллипса равна заданной константе. В данном случае, эллипс задан графически, и нам нужно найти точку, для которой произведение фокальных радиус-векторов будет равно квадрату малой полуоси.
Давайте обозначим фокусы эллипса как F1 и F2.
Шаг 1: Найти фокальные радиус-векторы
Фокальный радиус-вектор - это вектор, идущий из фокуса до точки на эллипсе. Для нахождения фокальных радиус-векторов, нам нужно найти координаты фокусов F1 и F2 и координаты точки на эллипсе.
На графике мы видим, что фокусы находятся на оси x, и позиции (a, 0) и (-a, 0), где a - большая полуось эллипса. Значит, координаты фокусов F1(a, 0) и F2(-a, 0).
Координаты данной точки на эллипсе обозначим как (x, y).
Шаг 2: Произведение фокальных радиус-векторов
Теперь, для данной точки на эллипсе, нам нужно найти произведение ее фокальных радиус-векторов.
Фокальный радиус-вектор от F1 до точки (x, y) можно записать как радиус-вектор RF1 = (x - a, y).
Фокальный радиус-вектор от F2 до точки (x, y) можно записать как радиус-вектор RF2 = (x + a, y).
Тогда произведение фокальных радиус-векторов будет равно RF1 * RF2 = (x - a)(x + a, y).
Шаг 3: Найти точку для которой произведение радиус-векторов равно квадрату малой полуоси
Теперь, мы знаем, что произведение фокальных радиус-векторов должно быть равно квадрату малой полуоси эллипса, то есть:
(x - a)(x + a, y) = b^2, где b - малая полуось эллипса.
Мы можем раскрыть скобки и упростить выражение:
x^2 - a^2y = b^2.
Таким образом, искомая точка на эллипсе имеет координаты (x, y), которые удовлетворяют уравнению x^2 - a^2y = b^2.
Это уравнение задает гиперболу, и только точки, лежащие на этой гиперболе, удовлетворяют условию задачи.
Для конкретных численных значений a и b, можно решить это уравнение и найти координаты точек на эллипсе. Для каждого значения a и b будет существовать две таких точки - по одной из каждой стороны оси x.
Надеюсь, это объяснение помогло понять, как найти точку на эллипсе, для которой произведение фокальных радиус-векторов равно квадрату малой полуоси. Если у вас остались какие-либо вопросы, пожалуйста, не стесняйтесь задать их!