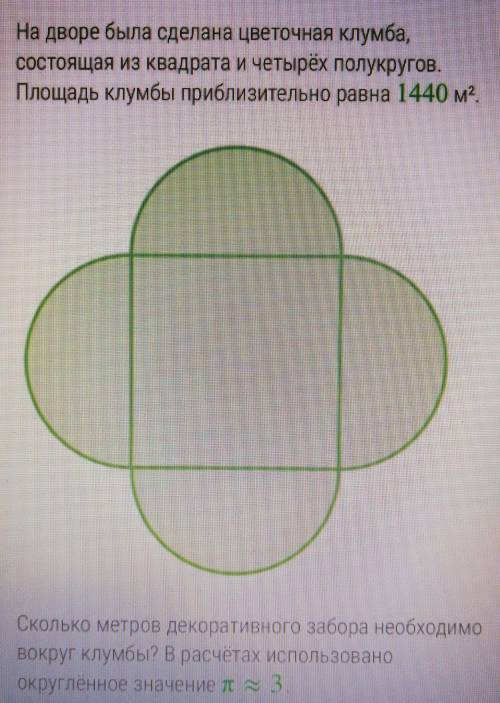
На дворе была сделана цветочная клумба,
состоящая из квадрата и четырёх полукругов.
Площадь клумбы приблизительно равна 1440 м^2?.
Сколько метров декоративного забора необходимо
вокруг клумбы? В расчетах использовано
округленное значение пи ≈ 3​

Для решения данной задачи можно разделить клумбу на составляющие ее фигуры и вычислить площадь каждой из них. Затем найдем периметр каждой фигуры и сложим их, чтобы определить общую длину забора.

Первым шагом определим площадь клумбы. Учитывая, что клумба состоит из квадрата и четырех полукругов, можно записать уравнение для площади клумбы:

Площадь квадрата + площади полукругов = 1440 м^2

Обозначим сторону квадрата через "a". Тогда площадь квадрата равна a^2.
Обозначим радиус полукружков через "r". Тогда площадь каждого полукруга равна 1/2 * π * r^2.

Теперь запишем уравнение для площади клумбы:

a^2 + 4 * (1/2 * π * r^2) = 1440

Так как в задаче указано, что используется округленное значение π ≈ 3, заменим его в уравнении и упростим:

a^2 + 2 * 3 * r^2 = 1440
a^2 + 6r^2 = 1440

Теперь найдем периметр каждой фигуры. Для квадрата периметр равен 4a, а для полукруга периметр равен πr + 2r.

Запишем уравнение для общей длины забора:

4a + 4 * (πr + 2r) = L

Используя значение π ≈ 3, получим:

4a + 4 * (3r + 2r) = L
4a + 4 * 5r = L
4a + 20r = L

Теперь остается только решить систему уравнений:

a^2 + 6r^2 = 1440
4a + 20r = L

Для этого можно воспользоваться различными методами, например, методом замены или методом сложения и вычитания. Выбор метода зависит от предпочтений и уровня подготовки школьника.

Решив систему уравнений, школьник найдет значения a и r. Подставив их в уравнение для общей длины забора, можно получить искомое значение L. Обязательно следует проверить правильность решения, подставив найденные значения в уравнение для площади клумбы, чтобы убедиться, что величина 1440 м^2 достигнута.

После этого, можно объяснить школьнику, что декоративный забор должен идти вокруг всей клумбы, следовательно, его длина равна L. Полученное значение L в метрах и будет ответом на задачу.

Надеюсь, данное разъяснение поможет школьнику понять решение задачи и выполнить ее самостоятельно.