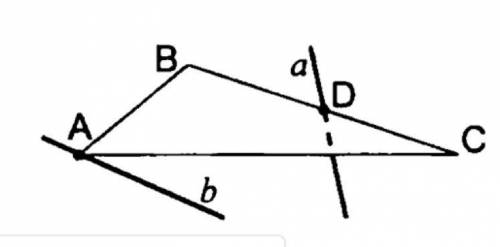
На чертеже прямые b и BC параллельны и прямая а не принадлежит плоскости (АВС). Докажите, что прямые а и b скрещивающиеся.
Другие вопросы по теме Геометрия
Популярные вопросы
- Подскажите аргументы из на тему что такое настоящая дружба? в сочинении...
3 - Определители объем газа( при нормальных условиях) выделившегося при...
3 - Почему в 1941 году шпиль был покрыт чехлом...
1 - Написать о войне. если можно не большой.√...
1 - Розбір слова за будовою слово писати...
3 - Как изображены дети, бегущие вслед за поездом в рассказе возвращение...
2 - 15 ! разобрать слова: лес, ряд. фонетический...
3 - Составь вопрос . и ответ 1 where/go? 2when? 3how/travel? 4what/do?...
1 - Из каких слагаемых состоит успех в жизни?...
1 - Диаметр ав делит каждую из хорд mn и pk отличных от диаметра пополам....
1
Рассмотрим треугольник ABC, образованный прямыми a, b и BC.
Поскольку прямые а и b пересекаются, они образуют угол. Пусть это будет угол α.
Из условия задачи известно, что прямые b и BC параллельны. Из свойств параллельных прямых следует, что углы α и β, где β - угол между прямыми b и BC, равны.
Также, поскольку прямая а не принадлежит плоскости ABC, она пересекает плоскость вне треугольника ABC.
Рассмотрим точку M, в которой прямая а пересекает прямую BC.
Поскольку прямые а и b пересекаются, углы α и β между прямыми a и b равны друг другу.
Тогда можно рассмотреть треугольник AMC, в котором есть два равных угла α и β.
По теореме о равных углах (пересекаемые прямые и углы) в треугольнике AMC можно заключить, что противоположные стороны этого треугольника также равны.
То есть, AC = CM.
Однако, согласно условию задачи, прямая а не лежит в плоскости ABC. Поэтому, точка C, в которой прямая а пересекает прямую BC, должна находиться вне треугольника ABC.
Так как AC = CM, а точка C находится вне треугольника ABC, получается противоречие.
Это значит, что предположение о пересечении прямых а и b неверно и прямые а и b скрещиваются.
Таким образом, доказано, что прямые а и b скрещивающиеся.