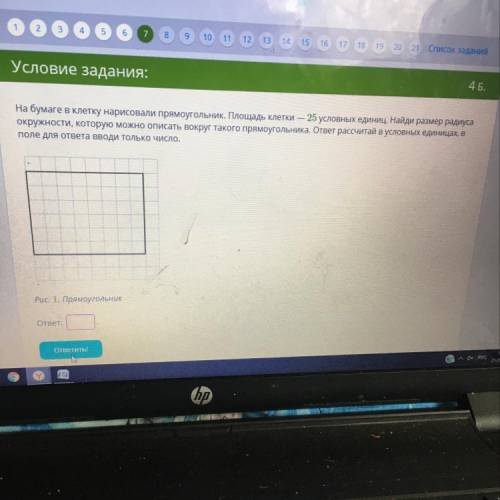
На бумаге в клетку нарисовали прямоугольник. Площадь клетки — 25 условных единиц. Найди размер радиуса
окружности, которую можно описать вокруг такого прямоугольника. ответ рассчитай в условных единицах, в
поле для ответа вводи только число.

Чтобы найти размер радиуса окружности, которую можно описать вокруг данного прямоугольника, нам нужно знать его характеристики. В данной задаче известна площадь прямоугольника, которая равна 25 условным единицам.

Площадь прямоугольника можно выразить через формулу: площадь = длина * ширина. Если обозначить длину прямоугольника за а, а ширину за b, то у нас получится уравнение: а * b = 25.

Также, известно, что окружность, описанная вокруг прямоугольника, имеет диаметр, равный длине прямоугольника. То есть, диаметр D = a.

Зная диаметр, мы можем найти радиус R, используя формулу: R = D / 2.

В данной задаче диаметр равен длине прямоугольника a, поэтому радиус будет равен радиусу равному R = a / 2.

Теперь, для того чтобы найти размер радиуса, нам нужно решить систему уравнений, которая состоит из уравнений площади прямоугольника и радиуса окружности:
1. a * b = 25 - уравнение площади прямоугольника.
2. R = a / 2 - уравнение размера радиуса.

Из уравнения 2, мы можем выразить длину прямоугольника a, как a = 2R.

Подставляя значение a в уравнение 1, получим: 2R * b = 25.

Теперь нам нужно найти значение ширины прямоугольника b. Решим уравнение относительно b:
b = 25 / (2R).

Таким образом, мы получили выражение ширины прямоугольника b через радиус R.

Итак, ответ на вопрос, как найти размер радиуса окружности, будет следующим: значение радиуса R вычисляется по формуле R = a / 2, где a - длина прямоугольника, а - 2R. Ширина прямоугольника b находится по формуле b = 25 / (2R).

Для нахождения конкретного численного значения радиуса R, необходимы конкретные численные значения длины и ширины прямоугольника. Информация о размерах прямоугольника не предоставлена в задаче, поэтому невозможно точно определить значение радиуса окружности.