На боковых сторонах ab и cd трапеции abcd взяты точки m и n так, что отрезок mn параллелен основаниям и делит площадь трапеции на пополам. найдите длину mn если bc=a и ad=b
Другие вопросы по теме Геометрия
Популярные вопросы
- Чем были вызваны народные выступления ? какие они повлияли на внутреннюю...
3 - Какой вид выветривания оказывает большое влияние на поверхность земли?...
3 - А4. в извитом канальце нефрона происходит полная реабсорбция 1) мочевины...
3 - Почему гоголь писал комедию «ревизор» сквозь слезы? я так предполагаю,...
1 - Перевести на произношение: five fat sausages frying in a pan all of a...
2 - Водну цепь включены электрическая лампа и электрическая плита сила тока...
3 - Чем обьясняется богатство индии гидроресурсами?...
3 - Найдите радиус круга, длинна которого равна 25,12 см(в квадрате)...
2 - Срешением уравнения: а) 5(х-3)=14-2(7-2х) б) 4х в квадрате + 7х =0...
2 - Знайти розв язку нерівності d + 36 42...
2
S(ABCD) = (a+b)*H/2
S(AMND) = (b+x)*h/2 = (a+b)*H/4
S(MBCN) = (a+x)*(H-h)/2 = (a+b)*H/4
Выразив h из второго уравнения и подставив в третье, получим:
(a+x)(2b+2x-a-b) = (a+b)(b+x)
2x^2 = a^2 + b^2
x = кор( (a^2 + b^2)/2)
Так как отрезок МN параллелен основаниям трапеции и разбивает ее на две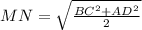 .
.
равновеликие трапеции, он является средним квадратичным для оснований
трапеции. И находится он по формуле: