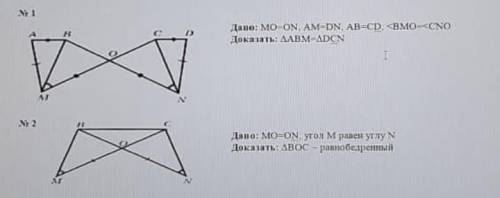
N 1 даво: MO-ON AM-DN, AB=CD. <BMO-<CNO
Докатать: ДАВМ-ADCN

Дано: MO=ON, угол М реп углу N
Докатать: АВОС - Равнобедренный

№1

Рассмотрим △MBO и △NCO, у которых: ∠BMO = ∠CNO, MO = NO (по условию) и ∠BOM = ∠CON как вертикальные углы при пересечении прямых BN и MC. Тогда △MBO = △NCO по 2 признаку равенства треугольников (по стороне и двум прилежащим к ней углам). Тогда из равенства треугольников получаем: MB = NC.

Рассмотрим треугольники △ABM и △DCN у которых AM = DN, AB = CD (по условию) и MB = NC. Тогда △ABM = △DCN по 3 признаку равенства треугольников (по трем сторонам), что и требовалось доказать.

№2

Рассмотрим △MBO и △NCO у которых: MO = ON, ∠M = ∠N,

∠BOM = ∠CON (как вертикальные углы при пересечении прямых BN, MC). Тогда △MBO = △NCO по 2 признаку равенства треугольников (по стороне и двум прилежащим к ней углам). Тогда из равенства треугольников получаем: BO = CO.

Рассмотрим △BOC,у которого BO = CO, тогда данный треугольник является равнобедренным по определению что и требовалось доказать.