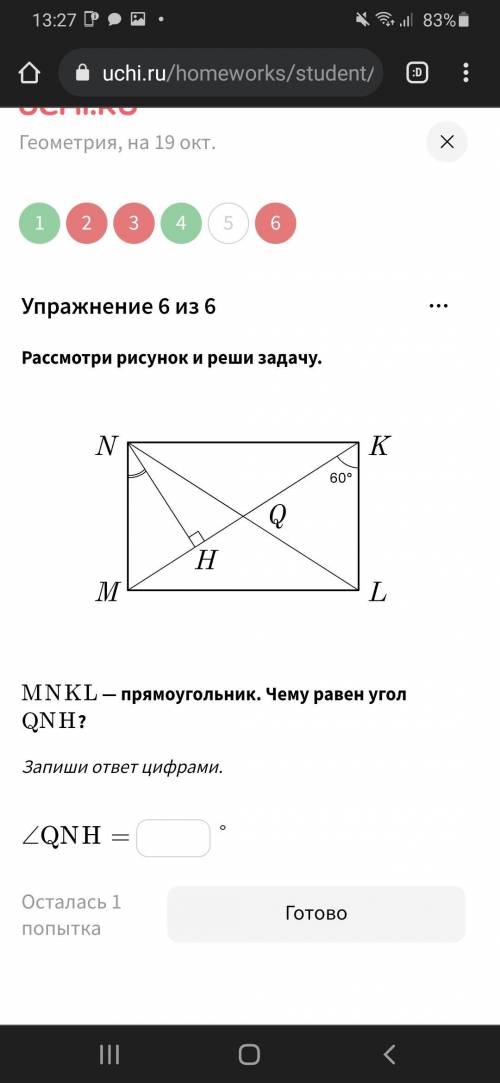
MNKL - прямоугольник. Чему равен угол QNH?
Другие вопросы по теме Геометрия
Популярные вопросы
- Вкабинете, тесно заставленном книгами, ярко горели две большие...
3 - Что происходит в ре мажоре гармоническом ? какой знак поставить...
2 - Сколько будет две целых три пятых плюс три целых две пятых икс...
2 - Определение польского вопроса во время правления николая 1? ?...
3 - Составь словосочетания.обозначь главное и зависимое слова.укажи,...
3 - Чем полезно молодое нужен вывод 10 , ответьте...
3 - Вбиблиотеки в одном читальном зале поставили 8 новых столов и...
3 - ///. закончите предложения: 1. she will play . a) next weekend...
1 - Сокол гриб солнце цветок снежинка петух какие из них живая природа...
2 - Втреугольнике pkf наименьшим углом является угол? , если сторона...
1
ответ: 30°
Объяснение: NMKL - прямоугольник. Диагонали прямоугольника равны и точкой пересечения делятся пополам. NL=MK, MQ=QK=QL. =>
∆ KQL – равнобедренный, углы при основании KL=60° =>
угол KQL=60°, угол NQH=60° равен ему (вертикальный).
Сумма острых углов прямоугольного треугольника 90°, поэтому искомый угол QNH=90°-60°=30°.
Или иначе:
∆ MQN=∆ KQL, – он равносторонний, NH- его высота, медиана и биссектриса.
Угол QNH=MNH=60°:2=30°.