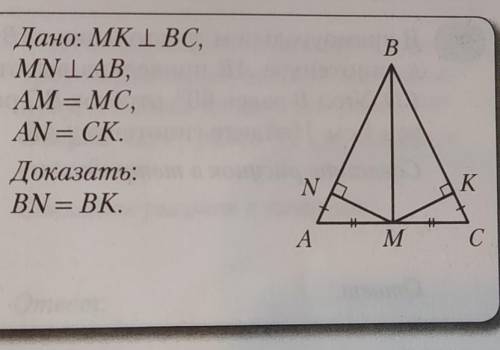
MK перпендикулярен BC MN перпендикулярен AB AM=MC AN=CK доказать BN=BK​

Дано: MK перпендикулярен BC, MN перпендикулярен AB, AM=MC, AN=CK.

Нам нужно доказать, что BN=BK.

Чтобы решить эту задачу, мы будем использовать свойства перпендикуляров и равных отрезков.

1. Рассмотрим треугольники AMN и CMB. У них углы МНА и МСВ прямые (так как есть перпендикуляры), и у нас есть две равные стороны согласно данным - AM=MC и MN=MB.

2. По свойству равных сторон треугольников, угол А равен углу С (так как AM=MC) и угол Н равен углу В (так как MN=MB).

3. Теперь рассмотрим треугольники ABN и CBK. У них две пары равных углов - угол А равен углу С и угол Н равен углу В.

4. Рассмотрим угол АМН. Поскольку угол МНА и угол НАМ - это прямые углы, сумма углов МНА и НАМ должна быть равна 180 градусов. Это означает, что угол АМН + угол НАМ = 180 градусов.

5. Аналогично, углы СМВ и АМС - это прямые углы, поэтому угол СМВ + угол АМС = 180 градусов.

6. Поскольку угол АМН + угол НАМ = угол СМВ + угол АМС и все эти углы равны 180 градусам, то угол АМН равен углу СМВ.

7. У нас есть два треугольника ABN и CBK с равными углами. Это означает, что они подобны друг другу по признаку сходности углов.

8. По свойству подобных треугольников, соответствующие стороны пропорциональны. Значит, BN/BK равно AB/CB.

9. Также, по данному условию, у нас есть равенство сторон AN=CK, поэтому BN/BK равно AN/CK.

10. Так как AN=CK и AB/CB равно BN/BK, то BN и BK равны между собой.

Таким образом, мы доказали, что BN равно BK.