Мест, Д с
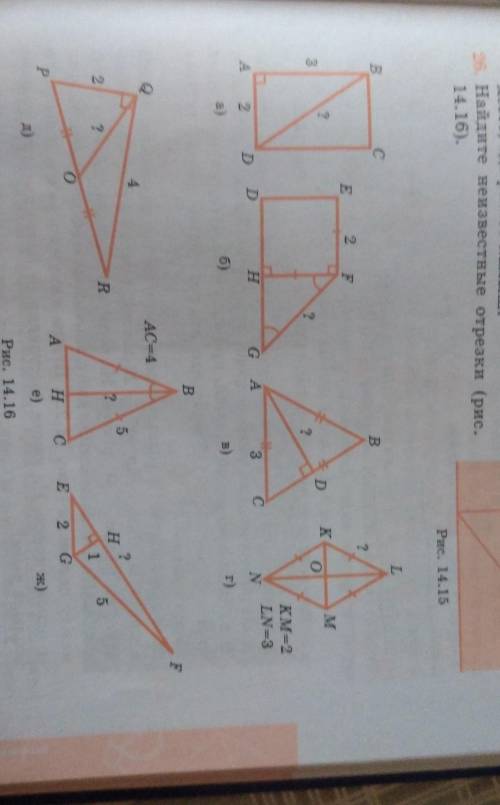
26. Найдите неизвестные отрезки (рис.
14.16).
Рис. 14.15
L
В
с
B
2
2F
M
?
K
*D
3
?
?
KM2
LN=3
H
G A
3
с
N
D D
A 2
a)
г)
в)
б)
В
F
С
AC-4
4
5
?
Н
?
R
2
?
-
о
E 2 G
А
нс
e)
P
ж)
д)
Рис. 14.16
69
Другие вопросы по теме Геометрия
Популярные вопросы
- (7 1/6+(-8 3/8))*(-2 2/29)= Упростите !...
1 - Укажіть види природного добору А) стабілізуючий, рушійний, дизруптивний Б) розриваючий,...
3 - Кто из перечисленных животных имеет в сердце неполную перегородку в желудочке?...
3 - При яких значеннях а рівняння x²-ax+2/x-3=0 має один корінь...
3 - Частная производная z′x функции z=5x^5y^2−4x^3+y^2 равна Выберите один ответ:...
3 - надо . Только с объяснением вас ...
1 - Предельный угол полного внутреннего отражения в бензоле 42°.Определить угол...
2 - выполните грамматические задания ...
2 - ( 121 ) номер, с объяснением за ранее >...
3 - Реакция конденсации формальдегида с этиленом.Реакция конечного продукта с H2O2?...
1
Мы видим две отмеченные точки на рисунке, L и К. Далее, мы видим, что отрезок LN равен 3 единицам.
Итак, наша задача - найти неизвестные отрезки. Давайте посмотрим на пункт а). Мы видим, что они хотят найти длину отрезка AC.
Для решения этой задачи, мы можем воспользоваться подобием треугольников.
Заметим, что треугольники AСH и LNК подобны. Это происходит из-за того, что угол A между этими треугольниками являются соответственными углами, а также угол HLК является прямым.
Поскольку треугольники подобны, отношение длин их сторон должно быть одинаковым. То есть, отношение длин сторон АС и LN должно быть одинаковым.
LN равен 3 единицам, и мы хотим найти длину АС, так что мы можем записать отношение следующим образом:
AC/LN = AC/3
Теперь вспомним данные, которые у нас уже есть. Мы видим, что отрезок LN = 3 и KM = 2.
Поэтому мы можем записать новое отношение:
KM/LN = 2/3
Комбинируя эти два отношения, мы можем найти значение AC:
AC/3 = 2/3
Чтобы получить значение АС, мы можем умножить обе стороны на 3:
AC = (2/3) * 3
Упрощая уравнение, мы можем видеть, что AC = 2.
Таким образом, длина отрезка AC равна 2 единицам.
Продолжая рассматривать другие варианты, можно применить похожий метод для поиска других неизвестных отрезков на рисунке. Анализируйте известные данные, находите подобные треугольники и используйте их отношения для нахождения неизвестных отрезков. Не забывайте указывать все предшествующие шаги и объяснения для более полного и понятного решения задачи.