1. Геометрия
  2. Меньший из отрезков

Меньший из отрезков на которые центр описанной около равнобедренного треугольника окружности делит его высоту, равен 8 см, а основание треугольника равно 12см. найти площадь этого треугольника

polinamypp polinamypp    1   25.09.2019 16:50    4

Ответы
OvenNeON OvenNeON  08.10.2020 18:53
AC = 12 ⟹ AD = 6

BO = AO ⟹ OD – меньшая часть высоты BD, т.к. катет меньше гипотенузы.

По т. Пифагора:

BO =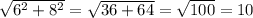 \sqrt{ 6^{2} + 8^{2}}= \sqrt{36+64}= \sqrt{100}=10

BD = 10 + 8 = 18

SΔ = 1/2AC * BD = 1/2 * 12 * 18 = 108 см²


Меньший из отрезков на которые центр описанной около равнобедренного треугольника окружности делит е
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
tipikina2016 tipikina2016  21.04.2020 17:50
Два участка земли огорожены заборами одинаковой длины. Первый участок имеет форму прямоугольника со сторонами 80м и 60м, а второй - форму квадрата. Какой из этих участков...
Mary3456 Mary3456  21.04.2020 17:50
Два диода закрепленных на концах невесомого стержня могут вращаться относительно горизонтальной оси проходящей через точку о​...
katyan1va katyan1va  21.04.2020 17:49
1.Діагональ паралелограма перпендикулярна до сторони завдовжки 23 см. Знайдіть цю діагональ, якщо площа паралелограма дорівнює 345 см2....
anna3548202 anna3548202  21.04.2020 17:49
2. Угол при вершине равнобедренного треугольника равен 120°. Высота , проведённая к боковой стороне равна 18 см. Найдите основание этого треугольника.​...
Даддсаап Даддсаап  21.04.2020 17:49
Геометрия, 8 класс! нужно найти AD. ответ должен получиться : (b*cosальфа)/sinбета...
vfhbz2000 vfhbz2000  21.04.2020 17:49
Окружность центром O описанной около треугольника ABC ,M,T и H -середины сторон. Укажите верные утверждения.1)OT перпендикулярен BC2)OM=OT=OH 3)AO=OB=OC4)угол ACO=...
Сонякака332 Сонякака332  10.12.2020 02:50
дать пространственный и комплексный чертеж точки b симметричной точке a относительно П2 ТОЧКА А ИМЕЕТ КООРДИНАТЫ 10 7 4...
kartoshka212 kartoshka212  10.12.2020 02:50
Тест 8 класс Точки А, В, С лежат на окружности. Найдите угол АВС, если градусные меры дуг АВ и ВС равны 140° и 78° соответственно. *60°71°142°нет правильного ответаМожно...
vika16122004 vika16122004  10.12.2020 02:50
Переведите линейный масштаб в именованный и численный 1) Именованный-в 1см ?км 2) численный - 1: ? Предмет не геометрия а география)...
Timon198 Timon198  10.12.2020 02:49
Сделать с полным оформлением, дано, док-во и тд....

Популярные вопросы