Меньшее основание трапеции ABCD равно 5см ,АВ=СD =8см , соsC = -3/4. Найдите площадь трапеции АВСD.

22√7

Объяснение:

Формула для нахождения площади трапеции через ее основания и высоту:

S =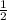 * (a + b) * h, где a, b — основания трапеции, h — высота трапеции.

СН ⊥ АД, СН - высота трапеции.

Рассмотрим ΔСДН(∠Н=90°).

СН = sin ∠Д * СД,

НД = cos ∠Д * СД.

Воспользуемся формулами приведения:

соsC = соs( 180°-∠Д) = - соs ∠Д ⇒ соs ∠Д = - соsC = 3/4

sin² ∠Д = 1 - соs² ∠Д = 1 - 9/16 = 7/16

sin ∠Д = = √7 / 4

СН = (√7 / 4 )* 8 = 2√7

НД = 3/4 * 8 = 6

т.к. трапеция АВСД - равнобокая, то АД = ВС+2*НД = 5+2*6=17 см

S =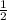 * (5+17)*  2√7 = 22√7

Есть 2 вариант.

После того, как нашли НД, через cos ∠Д, воспользоваться т. Пифагора и найти СН из ΔСДН :

СН² = СД²-НД² = 64-36 = 28

СН = √28= 2√7