Меньшее основание равнобедренной трапеции равно 12 см. Центр окружности, описанной около трапеции, находится на больше. основании, и ее радиус равен 10 см. Найди боковую сторону трапеции. Если в результате получилось иррациональное число, то запиши его в виде
и максимально вынеси из под знака корня полный квадрат.
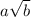
Другие вопросы по теме Геометрия
Популярные вопросы
- Масса 1 литра бензина 650 гр.в бензобак автомобиля входит 95 лит бензина...
3 - В3 одинаковых квартирах 15 комнат.на сколько больше комнат в 9 таких квартирах,чем...
2 - Формулы оксида,основания,кислоты соответственно записаны в ряду: а)croh,cro,h2po4;...
2 - 1.что такое серобород и что его осуществляет? 2.какие функции выполняет покрытосеменные...
3 - Выразите в более мелких единицах измерения 1ч= одна четвёртых часа= одна...
3 - Нужно написать письмо другу с новым годом...
1 - Изобразите на координатной прямой плоскости множество точек , координаты...
3 - 37 целых четыре пятых минус восемь целых 11 25 сколько будет...
3 - Расположите события описываемые в поэме илиада в хронологическом порядке...
1 - Составить и решить по условью; в теплице растут 550 гербер.это на 135 больше,чем...
2
Давайте разберемся пошагово:
1. У нас есть равнобедренная трапеция, у которой меньшее основание равно 12 см. Обозначим это меньшее основание как a.
a = 12 см
2. Центр окружности, описанной около трапеции, находится на большем основании. Предположим, что большее основание равно b.
3. Зная, что радиус окружности равен 10 см, мы можем использовать свойство равнобедренной трапеции, которое гласит, что высота равнобедренной трапеции является радиусом окружности, описанной около трапеции.
4. Высота равнобедренной трапеции равна 10 см. Обозначим ее как h.
5. Мы можем использовать теорему Пифагора для нахождения боковой стороны трапеции. Теорема Пифагора гласит, что для прямоугольного треугольника квадрат длины гипотенузы равен сумме квадратов длин катетов.
6. В нашем случае, боковая сторона трапеции является гипотенузой, а высота и половина разности оснований являются катетами.
7. Таким образом, мы можем записать следующее уравнение:
h^2 = a^2 - ((b - a)/2)^2
8. Подставим известные значения:
10^2 = 12^2 - ((b - 12)/2)^2
9. Раскроем скобки и упростим уравнение:
100 = 144 - (b - 12)^2/4
10. Перенесем все слагаемые на одну сторону уравнения:
(b - 12)^2/4 = 144 - 100
(b - 12)^2/4 = 44
11. Умножим обе части уравнения на 4, чтобы избавиться от деления:
(b - 12)^2 = 44 * 4
(b - 12)^2 = 176
12. Возведем обе части уравнения в квадратный корень:
sqrt((b - 12)^2) = sqrt(176)
b - 12 = sqrt(176)
13. Добавим 12 к обеим сторонам уравнения:
b = sqrt(176) + 12
14. Теперь найденное значение b является большим основанием трапеции. Возможно, оно окажется иррациональным числом.
15. Для нахождения боковой стороны трапеции нам нужно рассмотреть половину разности оснований, то есть (b - a)/2.
16. Подставим найденные значения:
(sqrt(176) + 12 - 12)/2 = sqrt(176)/2
17. После упрощения получим:
sqrt(176)/2 = (sqrt(16) * sqrt(11))/2
18. Мы знаем, что sqrt(16) = 4, поэтому можем заменить в уравнении:
(4 * sqrt(11))/2 = 2 * sqrt(11)
19. Итак, боковая сторона трапеции равна 2 * sqrt(11) см.
Запишем ответ в виде