M
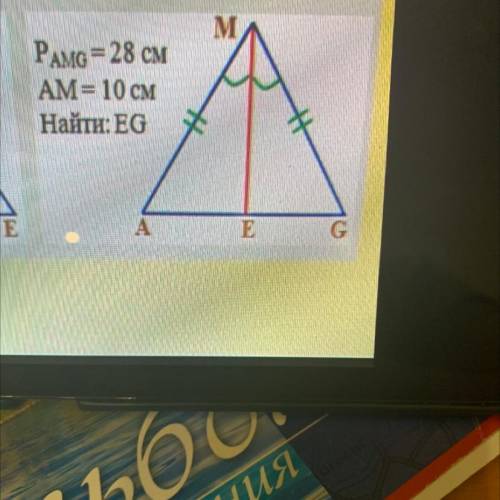
PAMG = 28 CM
AM= 10 CM
Найти : EG

EG=4см

Объяснение:

РAMG=AG+2AM

AG=PAMG-2AM=28-2*10=8см

МЕ- биссектрисса, медиана и высота в ∆АМG.

ЕG=AE

EG=AG:2=8:2=4см

Для решения этой задачи, нам нужно использовать свойства параллелограмма.

Свойство 1: В параллелограмме противоположные стороны равны.
Это означает, что сторона EG равна стороне MP. Поэтому EG = 28 см.

Свойство 2: В параллелограмме противоположные углы равны.
Это означает, что угол PAM равен углу GMG.

Теперь посмотрим на треугольник MPG. У нас есть данные, что сторона AM = 10 см, а сторона MP = 28 см.

Свойство 3: В треугольнике сумма длин двух сторон всегда больше третьей стороны.
Давайте проверим, выполняется ли это свойство для треугольника MPG.
10 + 28 > MP
38 > MP

Так как сумма сторон AM и MP больше, чем MP, то значит угол PAM является острым углом. Поскольку угол PAM равен углу GMG, то и угол GMG является острым углом.

Таким образом, EG = 28 см, и угол GMG является острым углом.