люди добрые, вроде легко, но я тупой.

Если не сложно, напишите с дано

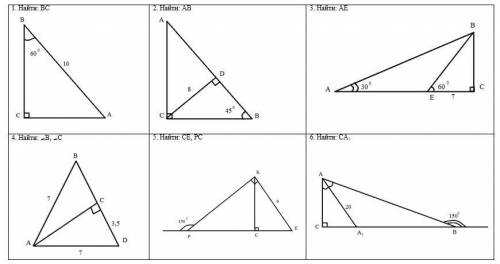
1. Дано: прямΔАВС с гипотенузой АВ; АВ=10, ∠СВА=60°;

Найти: ВС-?

Решение: ∠ВАС=90°-60°=30°, ВС - катет, лежащий против угла в 30°, он равен половине гипотенузы ВА, т.е. 5.

ответ: 5.

2. Дано: прямΔАВС с гипотенузой АВ; ∠АВС=45°, высота СD=8;

Найти: АВ-?

Решение: ΔАВС р/б, ∠САВ=45° (90°-45°); высота CD является медианой для гипотенузы АВ. По свойству, CD=1/2АВ. Т.е. АВ=16.

ответ: 16.

3. Дано: прямΔАВС с гипотенузой АВ; ∠ВАС=30°;

mЕ∈АС, ∠ВЕС=60°, ЕС=7;

Найти: АЕ-?

Решение: ∠ЕВС=90°-60°=30°, ЕС - катет, лежащий против угла в 30°, он равен половине гипотенузы ВЕ, т.е. ВЕ=14. ∠АВС=90°-∠ВАС=60°. Т.е. ∠АВЕ=60°-∠ЕВС=30°, ⇒ ΔАВЕ р/б, т.к. ∠ВАЕ=∠АВЕ, ⇒АЕ=ВЕ=14.

ответ: 14.

4. Дано: р/б ΔАВD с основанием ВD, АС - высота, CD=3.5см;

Найти: ∠В и ∠С;

Решение: АС⊥ВD, значит ∠ВСА=90°. АС является медианой для ВD, т.к. проведена к основанию, ⇒ ВС=3.5. АВ=1/2ВС, ⇒ ∠ВАС=30°, ⇒ ∠АВС=90°-30°=60°.

ответ: 60°, 90°.

5. Дано: прямΔРКЕ с гипотенузой РЕ; внеш.уг. при вершине Р=150°; КЕ=9; КС-высота;

Найти: РС и СЕ;

Решение: ∠КЕР=150°-90°=60° (св-во внеш. уг.); ∠СКЕ=90°-60°=30°, ⇒ СЕ - катет, лежащий против угла в 30°, он равен половине гипотенузы КЕ, ⇒ СЕ=9:2=4.5. ∠КРЕ=180°-150°=30° (смеж.уг.); КЕ - катет, лежащий против угла в 30°, он равен половине гипотенузы РЕ, ⇒ 9*2=18. РЕ=РС+СЕ, ⇒ РС=18-4.5=13.5.

ответ: 13.5 - РС, 4.5 - СЕ.

6. Дано: прямΔСАВ с гипотенузой АВ; внеш. уг. при вершине В=150°; АА₁-биссектриса ∠САВ; АА₁=20;

Найти: СА₁;

Решение: ∠САВ=150°-90°=60° (св-во внеш. уг.); ∠САА₁=1/2∠САВ, ⇒ ∠САА₁=60°:2=30°; СА₁ - катет, лежащий против угла в 30°, он равен половине гипотенузы АА₁, ⇒ СА₁=20:2=10.

ответ: 10.

Добрый день! Конечно, я готов помочь вам разобраться с вашим вопросом.

Итак, у нас есть дано:

1. Квадрат ABCD со стороной 4 см.
2. Отрезок AE, который является диагональю квадрата ABCD.
3. Отрезок AB, который является прямой наатегорией с отрезком AE.
4. Отрезок BF, который является прямой наатегорией с отрезком AE и продолжается за ним.

Наша задача: найти длину отрезка EF.

Давайте разберемся пошагово:

1. Обратим внимание на прямые нацопи, которые проходят через отрезок AE.

2. Поскольку мы знаем, что квадрат ABCD является квадратом, то его углы, включая угол A, равны 90 градусам. Также известно, что отрезок AB является прямой нацопи с отрезком AE, поэтому угол EAB также равен 90 градусам.

3. Мы знаем, что треугольник ABE является прямоугольным треугольником. Так как угол EAB равен 90 градусам, радиус отрезка AE совпадает с радиусом отрезка AB или BF.

4. Таким образом, отрезок AE и AB имеют одинаковую длину, которая равна 4 см.

5. Теперь нам нужно найти длину отрезка EF. Мы знаем, что отрезок AB делит отрезок AE на две равные части, поэтому длина отрезка AE равна сумме длин отрезков AB и BF.

6. Следовательно, длина отрезка EF равна разности длин отрезков AE и AB, то есть 4 см минус 4 см, что равно 0 см.

Таким образом, длина отрезка EF равна 0 см.

Надеюсь, это объяснение было понятным для вас. Если у вас возникли еще вопросы, не стесняйтесь задавать их.