Люди ! 2) MNKP — параллелограмм. Его смежные стороны равны 40 40 см и 68 см, диагональ — 84 см. Найди его площадь. Вырази ответ в см 2
3) Дана трапеция MNKL , у которой MN= 5, NL = 29, ML = 30MN=5,NL=29,ML=30 . Найди площадь данной трапеции, если NK = 16NK=16 .
4) Дан треугольник MNK , у которого MN =18, NK=24, KM=30MN=18,NK=24,KM=30 . Чему равна высота, проведённая из точки K K к стороне MNMN ?
5) Дан ромб PRTD . Его сторона равна 4141 см, а диагональ — 18 18 см. Найди площадь треугольника, образованного двумя сторонами ромба и данной диагональю. Вырази ответ в см ^2
ПРОСТО НЕ НАДО РЕШЕНИИ ДАЙТЕ ПРОСТО ОТВЕТЫ и ВСЕ
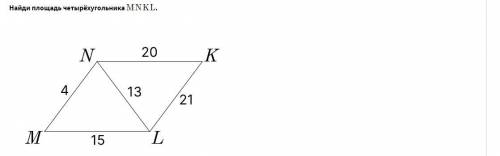

Другие вопросы по теме Геометрия
Популярные вопросы
- Проанализируйте внешнеполитические события 1820— 1840-х годов. Подумайте,...
3 - Какие уроки должна была извлечь Россия из Крымской войны?...
1 - Как вы поняли термин « восточный вопрос »? Можно ли решение «восточного...
2 - Проанализируйте материал об общественном движении 1830-1840-х годов и...
2 - Сравните причины и итоги русско-иранских войн 1804— 1813 годов и 1826-1828...
1 - Какие последствия для России, на ваш взгляд, имели незыблемая вера Николая...
3 - В разговоре с американским посланником Джорджем Далласом император Николай...
1 - Какие цели преследовала Россия в русско-турецкой войне 1828-1829 годов?...
1 - Как соотносится заявление императора Николая I о том, что Россия «никогда...
2 - Как бы вы оценили поступок императора Николая I во время «холерного бунта»...
3
2) У нас есть параллелограмм MNKP с смежными сторонами, равными 40 см и 68 см, и диагональю длиной 84 см. Нам нужно найти площадь этого параллелограмма.
Площадь параллелограмма можно найти по формуле: площадь = база * высоту.
Найдем высоту параллелограмма. Возьмем диагонали параллелограмма и разделим его на 2, чтобы получить высоту. Значит, высота равна половине диагонали, то есть 84 см / 2 = 42 см.
Теперь у нас есть высота и смежные стороны параллелограмма. Положим одну из смежных сторон в качестве базы и умножим ее на высоту: 40 см * 42 см = 1680 см^2.
Ответ: площадь параллелограмма MNKP равна 1680 см^2.
3) Теперь нам нужно найти площадь трапеции MNKL с данными сторонами и основаниями. У нас есть основания MN и KL, высоту NK и длину NL.
Формула для нахождения площади трапеции: площадь = (сумма оснований * высота) / 2.
Сумма оснований равна MN + KL = 5 + 29 = 34.
Также у нас есть высота NK, которая равна 16.
Подставим все значения в формулу: площадь = (34 * 16) / 2 = 544 / 2 = 272 см^2.
Ответ: площадь трапеции MNKL равна 272 см^2.
4) Переходим к треугольнику MNK. Нам нужно найти высоту, проведенную из точки K к стороне MN.
Высота треугольника - это отрезок, опущенный из одной из вершин до противолежащей стороны и перпендикулярный этой стороне.
Для нахождения высоты треугольника MNK можно использовать формулу для площади треугольника: площадь = (основание * высота) / 2.
В нашем случае, высота треугольника равна высоте, проведенной из точки K, и она неизвестна. У нас есть стороны MN и NK, и мы можем использовать их для нахождения высоты.
Давай воспользуемся формулой Пифагора чтобы найти отсутствующую сторону. По теореме Пифагора: гипотенуза^2 = катет1^2 + катет2^2.
Возьмем стороны MN и NK как катеты и KM как гипотенузу: KM^2 = MN^2 + NK^2.
Подставим известные значения: KM^2 = 18^2 + 24^2 = 324 + 576 = 900.
Теперь найдем KM, извлекая квадратный корень из обеих сторон: KM = √900 = 30.
Теперь у нас есть стороны MN, NK и KM. Подставим их в формулу для высоты треугольника: площадь = (MN * высота) / 2.
Решим уравнение относительно высоты: (18 * высота) / 2 = площадь.
Теперь выразим высоту: высота = (2 * площадь) / 18 = (2 * площадь) / (2 * 9) = площадь / 9.
Ответ: высота, проведенная из точки K к стороне MN, равна площади треугольника MNK, деленной на 9.
5) Наконец, у нас есть ромб PRTD со стороной 41 см и диагональю 18 см. Нам нужно найти площадь треугольника, образованного двумя сторонами ромба и данной диагональю.
Площадь треугольника можно найти по формуле Герона. Формула Герона представляет собой сумму площадей треугольников, образованных сторонами треугольника и полупериметром треугольника.
Первым делом, найдем полупериметр треугольника. Чтобы найти полупериметр, сложим все стороны треугольника и разделим полученную сумму на 2: полупериметр = (сторона1 + сторона2 + сторона3) / 2 = (сторона1 + сторона2 + сторона1) / 2 = (41 + 41 + 18) / 2 = 100 / 2 = 50.
Теперь используем формулу Герона для нахождения площади треугольника: площадь = √(полупериметр * (полупериметр - сторона1) * (полупериметр - сторона2) * (полупериметр - сторона3)).
Подставим известные значения и рассчитаем площадь: площадь = √(50 * (50 - 41) * (50 - 41) * (50 - 18)) = √(50 * 9 * 9 * 32) = √(129600) = 360.
Ответ: площадь треугольника, образованного двумя сторонами ромба и данной диагональю, равна 360 см^2.
Надеюсь, мои объяснения были понятны и помогли разобраться с решением задач. Если у тебя остались вопросы, не стесняйся задавать их!